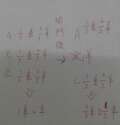[歡樂惡搞]無題 無名 21/01/10(日)05:10:51 ID:deSZ0/4s No.2184712
評分:0, 年:0, 月:0, 週:0, 日:0, [+1 / -1] 最後更新:2021-01-17 17:27:21
無本文
無題 無名 21/01/10(日)07:21:54 ID:61DaW.TU No.2184719
>>2184712
幹哩不播完是怎樣
幹哩不播完是怎樣
無題 無名 21/01/10(日)12:31:45 ID:Rnp/YTwU No.2184772
無題 無名 21/01/10(日)16:08:07 ID:WsZR5Ep6 No.2184811
>>2184766
你上次竟然沒有選母山羊
你上次竟然沒有選母山羊
>>2184804
換了會中的機率比較大,但你也可以選擇不相信機率
換了會中的機率比較大,但你也可以選擇不相信機率
無題 無名 21/01/10(日)20:27:30 ID:iDAw0426 No.2184850
下禮拜面試新人就考這個好了
無題 無名 21/01/10(日)20:50:33 ID:i7OdZ/K6 No.2184855
我記得這東西是一開始選的時候選到車機率是1/3
主持人開一扇門後再來選會變1/2
如果重選的話選到車機率是1/2
不重選機率就是1/3
所以應該要重選這樣機率比較大
......我只覺得是在玩文字遊戲就是了
主持人開一扇門後再來選會變1/2
如果重選的話選到車機率是1/2
不重選機率就是1/3
所以應該要重選這樣機率比較大
......我只覺得是在玩文字遊戲就是了
無題 無名 21/01/10(日)21:29:39 ID:Ybv7uem. No.2184871
無題 無名 21/01/10(日)21:31:14 ID:5B3C1JWU No.2184872
https://youtu.be/kIo0EpetyEw
無題 無名 21/01/10(日)21:32:47 ID:VeN6IzjU No.2184875
>>2184868
https://zh.wikipedia.org/wiki/%E8%92%99%E6%8F%90%E9%9C%8D%E7%88%BE%E5%95%8F%E9%A1%8C
由當時最聰明的女性Marilyn vos Savant破解
https://zh.wikipedia.org/wiki/%E8%92%99%E6%8F%90%E9%9C%8D%E7%88%BE%E5%95%8F%E9%A1%8C
由當時最聰明的女性Marilyn vos Savant破解
>>2184868
......
你一開選的時候中獎機率是1/3
如果你堅持不換 不管主持人有沒有做開門這個動作 你的機率始終是1/3
因為主持人開門與否並不會影響你中獎的機率
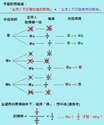
如果你在主持人開門後堅持換剩下那扇門的話有三種可能
(1)你一開始就選中汽車 主持人給你看山羊A或B其中一隻 結果你換成了另一隻山羊
(2)你一開使選中山羊A 主持人給你看山羊B 結果你換成了汽車
(3)你一開使選中山羊B 主持人給你看山羊A 結果你換成了汽車
以上三種可能機率都是一樣的 因此你的中獎機率變成2/3
這不是在玩文字遊戲 而是主持人幫你刪去了不是大獎的那扇門
但只有你願意換門 機率才會不一樣 否則始終中獎機率是1/3
還有另一種解釋 之前有位島民用100扇門來舉例
假如這次題目改為100扇門 只有1扇背後有汽車
不管你選哪扇 主持人都會打開98扇門只留下1扇門問你要不要換
如果你不換 中獎機率始終只有1/100
但如果換門因為主持人幫你刪去98扇不是大獎的門
只要你原本抽中山羊又選擇換門就一定能拿到汽車 因此你的中獎機率變為99/100
......
你一開選的時候中獎機率是1/3
如果你堅持不換 不管主持人有沒有做開門這個動作 你的機率始終是1/3
因為主持人開門與否並不會影響你中獎的機率
如果你在主持人開門後堅持換剩下那扇門的話有三種可能
(1)你一開始就選中汽車 主持人給你看山羊A或B其中一隻 結果你換成了另一隻山羊
(2)你一開使選中山羊A 主持人給你看山羊B 結果你換成了汽車
(3)你一開使選中山羊B 主持人給你看山羊A 結果你換成了汽車
以上三種可能機率都是一樣的 因此你的中獎機率變成2/3
這不是在玩文字遊戲 而是主持人幫你刪去了不是大獎的那扇門
但只有你願意換門 機率才會不一樣 否則始終中獎機率是1/3
還有另一種解釋 之前有位島民用100扇門來舉例
假如這次題目改為100扇門 只有1扇背後有汽車
不管你選哪扇 主持人都會打開98扇門只留下1扇門問你要不要換
如果你不換 中獎機率始終只有1/100
但如果換門因為主持人幫你刪去98扇不是大獎的門
只要你原本抽中山羊又選擇換門就一定能拿到汽車 因此你的中獎機率變為99/100
這該說是1/3的機率跟2/3的機率比較下來
只有1/3的差距會讓人產生迷樣的自信感嗎?
搞不好我1/3就猜對了 換了不就什麼都沒了
只有1/3的差距會讓人產生迷樣的自信感嗎?
搞不好我1/3就猜對了 換了不就什麼都沒了
無題 無名 21/01/10(日)22:04:33 ID:CaXBDypA No.2184884
無題 無名 21/01/10(日)22:14:25 ID:DFOABmUM No.2184889
>>2184887
倖存者偏差啦!
倖存者偏差啦!
無題 無名 21/01/10(日)22:28:18 ID:mMG9Lb/M No.2184894
無題 無名 21/01/10(日)22:46:15 ID:7XE4eqwY No.2184902
We are counting, not gambling
無題 無名 21/01/10(日)22:52:06 ID:HbBziH.. No.2184908
>>2184894
機率的東西自己做模型來測不就好了嗎
機率的東西自己做模型來測不就好了嗎
無題 無名 21/01/10(日)22:57:53 ID:OsYu2ddY No.2184913
>>2184894
你說得對
你說得對
其實不用想成機率這麼複雜
這遊戲的盲點在於主持人只會開有山羊的門
假設現在有一號門羊.二號門羊.三號門車
選了一,主持人會開有羊的二,換了就有車
選了二,主持人會開有羊的一,換了就有車
選了三,主持人會開有羊的一或二,換了會有羊
所以選換,會三選二中車,機率66%
這遊戲的盲點在於主持人只會開有山羊的門
假設現在有一號門羊.二號門羊.三號門車
選了一,主持人會開有羊的二,換了就有車
選了二,主持人會開有羊的一,換了就有車
選了三,主持人會開有羊的一或二,換了會有羊
所以選換,會三選二中車,機率66%
>>2184901
隔壁老王說他夢明牌夢到告訴我的。
你、貝葉斯、帕斯卡或著隔壁老王以及任何人在真理面前都是平等的
為何比較聰明的人講的就對的,而隔壁老王講的就錯呢
例如我們為何要去信一個沒沒無聞的波蘭教士的話
而不去信偉大的托勒密和他的天動說呢
天動說也是經由大量的幾何分析所得的理論啊
隔壁老王說他夢明牌夢到告訴我的。
你、貝葉斯、帕斯卡或著隔壁老王以及任何人在真理面前都是平等的
為何比較聰明的人講的就對的,而隔壁老王講的就錯呢
例如我們為何要去信一個沒沒無聞的波蘭教士的話
而不去信偉大的托勒密和他的天動說呢
天動說也是經由大量的幾何分析所得的理論啊
>>2184915
因為哥白尼有提出理論,還有伽利略、克卜勒來證明,而你只會聽隔壁老王夢明牌。
因為哥白尼有提出理論,還有伽利略、克卜勒來證明,而你只會聽隔壁老王夢明牌。
無題 無名 21/01/10(日)23:29:33 ID:CjyUeKFQ No.2184922
(換) 這個選項的中獎率是2/3
(不換) 這個選項的中獎率1/3
但若一個人沒想那麼多 換與不換的機率是1/2的話
那中獎率其實也是1/2
就好像他在(2/3中獎)跟(1/3中獎)的選項裡面1/2的機率隨機選一個
(不換) 這個選項的中獎率1/3
但若一個人沒想那麼多 換與不換的機率是1/2的話
那中獎率其實也是1/2
就好像他在(2/3中獎)跟(1/3中獎)的選項裡面1/2的機率隨機選一個
無題 無名 21/01/10(日)23:36:31 ID:CjyUeKFQ No.2184924
超容易理解版 參加這個活動100次
100次都換>>中獎期望值66次
100次都不換>>中獎期望值33次
前50次換 後50次不換>>中獎期望值50次
100次都換>>中獎期望值66次
100次都不換>>中獎期望值33次
前50次換 後50次不換>>中獎期望值50次
無題 無名 21/01/10(日)23:45:45 ID:VS8IgG4. No.2184926
幹!這問題我不知道是第幾次看到上島討論了
印象起碼有5次哦 其他版還不算
真是不懂也都被教到懂了
要是當初在學機率與統計有多花點時間去弄懂就好了
我發現學數學 對這種有用生活事物舉例人腦很容易就超捷徑跳步驟 用生活經驗去解釋
而不是依數學規則去解釋
印象起碼有5次哦 其他版還不算
真是不懂也都被教到懂了
要是當初在學機率與統計有多花點時間去弄懂就好了
我發現學數學 對這種有用生活事物舉例人腦很容易就超捷徑跳步驟 用生活經驗去解釋
而不是依數學規則去解釋
無題 無名 21/01/10(日)23:53:31 ID:mMG9Lb/M No.2184929
無題 無名 21/01/10(日)23:57:48 ID:fJcG47iU No.2184931
>>2184929
這裡是在討論數學而不是哲學
這裡是在討論數學而不是哲學
>>2184929
>>所以實驗證明1/3是錯的
換門後的中獎率是67%(約略2/3),不換是32%(約略1/3)
不要說數學邏輯,現在連讀寫都有問題了嗎
>>他說他的明牌夢上次讓他抽到刮刮樂
這叫偶然或是僥倖,完全沒有理論背書作夢跟中獎之間有直接關係,而數學理論有模型可以套用在不同狀況跟數值讓你反覆驗證因果關係
另外占星術廣義來說也可以是一種統計學,一定程度上確實可以統整出某種星座的人在性格上會有什麼傾向
跟血型性別分析差不多
會說錯的占星學你應該是指電視那種今天什麼座應該要幹嘛或是今年什麼座會怎麼樣的,那單純就是心理上的安慰或是純粹神棍
最後
>>就是因為認真才會問
我們都不是因為是聰明人說的話才信,而是看見數值之後心服口服
那怕今天的算是是流浪漢解讀出來的只要經過驗證你也不得不服
當年三門問題被Marilyn vos Savant解出來之後學界也因為違反直覺質疑過,但是算是一出來大家自己下來算也是不得不低頭承認
只有你自以為見解獨到拿老王的夢去質疑算式,這不叫認真
你只是腦袋抽筋而已
>>所以實驗證明1/3是錯的
換門後的中獎率是67%(約略2/3),不換是32%(約略1/3)
不要說數學邏輯,現在連讀寫都有問題了嗎
>>他說他的明牌夢上次讓他抽到刮刮樂
這叫偶然或是僥倖,完全沒有理論背書作夢跟中獎之間有直接關係,而數學理論有模型可以套用在不同狀況跟數值讓你反覆驗證因果關係
另外占星術廣義來說也可以是一種統計學,一定程度上確實可以統整出某種星座的人在性格上會有什麼傾向
跟血型性別分析差不多
會說錯的占星學你應該是指電視那種今天什麼座應該要幹嘛或是今年什麼座會怎麼樣的,那單純就是心理上的安慰或是純粹神棍
最後
>>就是因為認真才會問
我們都不是因為是聰明人說的話才信,而是看見數值之後心服口服
那怕今天的算是是流浪漢解讀出來的只要經過驗證你也不得不服
當年三門問題被Marilyn vos Savant解出來之後學界也因為違反直覺質疑過,但是算是一出來大家自己下來算也是不得不低頭承認
只有你自以為見解獨到拿老王的夢去質疑算式,這不叫認真
你只是腦袋抽筋而已
無題 無名 21/01/11(一)00:22:53 ID:PRHvf.As No.2184938
>>2184928
有些笨蛋就不喜歡承認自己很笨
有些笨蛋就不喜歡承認自己很笨
>>2184929
你把這個題目想像為總共有一百個門
當你選擇第一個門時,你的中獎機率為1%
那你沒中獎的機率就是99%
當主持人問你要不要交換時
就是再問你要不要從 1/100換到 98+1/100
如果你認為機率一樣都是50/50
可以自己做個小模型,先把門換成四個
那你的中獎機率就是25%(1/4),當你選擇交換則會變成75%(3/4)
五門就是20% : 80% 依此類推
當門的數量越多,你交換時的勝率就越高
你把這個題目想像為總共有一百個門
當你選擇第一個門時,你的中獎機率為1%
那你沒中獎的機率就是99%
當主持人問你要不要交換時
就是再問你要不要從 1/100換到 98+1/100
如果你認為機率一樣都是50/50
可以自己做個小模型,先把門換成四個
那你的中獎機率就是25%(1/4),當你選擇交換則會變成75%(3/4)
五門就是20% : 80% 依此類推
當門的數量越多,你交換時的勝率就越高
無題 無名 21/01/11(一)00:45:06 ID:zJSFFjbw No.2184944
>>2184894
自以為是說的就是你這種人,知道嗎?
自以為是說的就是你這種人,知道嗎?
無題 無名 21/01/11(一)00:47:05 ID:FfJhmy6E No.2184946
你一開始的選擇有三種可能
正確解答也有三種可能
所以有九種可能~~~而且發生機率都為九分之一
其中有三種可能是你一開始就猜中
換了門就失敗了
剩下六種可能是是你一開始沒猜中
主持人又幫你把一扇沒中的門開掉
剩下的那扇門當然是中獎的~換了就中
所以選擇換門~~中獎率是三分之二
選擇不換門~~就是無視主持人的事件影響
那機率就沒變動過~就是一開始的三分之一
正確解答也有三種可能
所以有九種可能~~~而且發生機率都為九分之一
其中有三種可能是你一開始就猜中
換了門就失敗了
剩下六種可能是是你一開始沒猜中
主持人又幫你把一扇沒中的門開掉
剩下的那扇門當然是中獎的~換了就中
所以選擇換門~~中獎率是三分之二
選擇不換門~~就是無視主持人的事件影響
那機率就沒變動過~就是一開始的三分之一
無題 無名 21/01/11(一)00:57:00 ID:2DTc31OU No.2184949
>>2184936
1/3是我筆誤,是我不對
但是66/100不等於2/3,就算約略2/3但也不是2/3
今天要是有另一個理論推斷出來說機率是66/100,是不是反而這個理論是更正確的?
要用理論背書理論永遠總是有的,老王也可以說做夢可以看到明牌是人的潛意識還是宇宙能量阿里阿雜造成的
就算多麼荒誕不稽理論也是理論,還是回到那句老話
我要怎麼確認常規的數學理論和老王的理論(以及背書理論的理論)哪個是正確的?
天動說也可以正確的預測天體運行,為什麼我們要改信地動說?
生醫領域的論文一大堆再現不出來的*,為什麼我們還是信任生物化學?
我也知道用常規的數學去計算出來答案就是那樣
但還是一樣,為什麼我們可以認為現實世界是按數學理論在運行的?
而不是按神的旨意或是老王的夢在運行的?
*https://www.thenewslens.com/article/129655
1/3是我筆誤,是我不對
但是66/100不等於2/3,就算約略2/3但也不是2/3
今天要是有另一個理論推斷出來說機率是66/100,是不是反而這個理論是更正確的?
要用理論背書理論永遠總是有的,老王也可以說做夢可以看到明牌是人的潛意識還是宇宙能量阿里阿雜造成的
就算多麼荒誕不稽理論也是理論,還是回到那句老話
我要怎麼確認常規的數學理論和老王的理論(以及背書理論的理論)哪個是正確的?
天動說也可以正確的預測天體運行,為什麼我們要改信地動說?
生醫領域的論文一大堆再現不出來的*,為什麼我們還是信任生物化學?
我也知道用常規的數學去計算出來答案就是那樣
但還是一樣,為什麼我們可以認為現實世界是按數學理論在運行的?
而不是按神的旨意或是老王的夢在運行的?
*https://www.thenewslens.com/article/129655
無題 無名 21/01/11(一)00:58:36 ID:2spGFGYg No.2184950
無題 無名 21/01/11(一)01:06:02 ID:jDp94USQ No.2184952
>>2184929
如果你是認真的問,我也試著認真向你解釋
首先其實你所謂對錯的定位已經有點錯
這不是一個對錯的問題
不是說你相信機率就一定對一定能贏大獎
相信直覺就一定錯一定輸大獎
原PO這是一個著名的機率命題:『蒙提霍爾問題』
不是天動說、不是地平論、不是隨便一個假裝專家說出來的騙人把戲
要比喻的話,你應該放他在地動說、地圓論這樣已經被學界公眾證明的存在
其次,我現在要解釋的是機率高低,不是憑直覺看彩數
如果只看彩數認為只有中與不中兩個結果,那當中的機率你不懂也吧
3門你比較難理解
就像上面一般,我先把門增加到100道
只有一道門有獎
你只能選一門,那中獎的可能性就是一百份之一(1/100)
一百門選一門,只有百份一的中獎機會
如果主持人沒開門不提供換門機會的話,你的中獎機率到結束都是1/100
好了,到這步你還明白嗎?
接下來,主持人開其餘98道沒獎的門,只留下一門跟你說換不換
如果不換,就跟上面說的一樣,機率不變,你一樣是等於一開始一百門中的一門,中獎可能是只有百份一(1/100)
但如果換了,因為你一開始中獎可能是只有百份一,這時候換的話機率就會對調,從1/100變成99/100,就等於你從百門中選了99道門,只是主持會開走98道沒中的門
所以不換,中獎率是1/100
換,中獎率是99/100
因此換,中獎率就變大
當然,你也可以是秋森萬
從一開始的100門中,一手就選中了中獎的那一門
這樣你換的話才會不中
然而,原PO的是3門,一開始選中的機率也有三份一(1/3)
從一開始你就選中也不是不可能的事
但就正如我上面說的
這是要解釋機率高低,不是憑直覺看彩數
就這樣,懂了嗎?
>>2184930
真正的電視遊戲主持人的確會這樣做
因為要保住大獎不能輕易送出
如果你是認真的問,我也試著認真向你解釋
首先其實你所謂對錯的定位已經有點錯
這不是一個對錯的問題
不是說你相信機率就一定對一定能贏大獎
相信直覺就一定錯一定輸大獎
原PO這是一個著名的機率命題:『蒙提霍爾問題』
不是天動說、不是地平論、不是隨便一個假裝專家說出來的騙人把戲
要比喻的話,你應該放他在地動說、地圓論這樣已經被學界公眾證明的存在
其次,我現在要解釋的是機率高低,不是憑直覺看彩數
如果只看彩數認為只有中與不中兩個結果,那當中的機率你不懂也吧
3門你比較難理解
就像上面一般,我先把門增加到100道
只有一道門有獎
你只能選一門,那中獎的可能性就是一百份之一(1/100)
一百門選一門,只有百份一的中獎機會
如果主持人沒開門不提供換門機會的話,你的中獎機率到結束都是1/100
好了,到這步你還明白嗎?
接下來,主持人開其餘98道沒獎的門,只留下一門跟你說換不換
如果不換,就跟上面說的一樣,機率不變,你一樣是等於一開始一百門中的一門,中獎可能是只有百份一(1/100)
但如果換了,因為你一開始中獎可能是只有百份一,這時候換的話機率就會對調,從1/100變成99/100,就等於你從百門中選了99道門,只是主持會開走98道沒中的門
所以不換,中獎率是1/100
換,中獎率是99/100
因此換,中獎率就變大
當然,你也可以是秋森萬
從一開始的100門中,一手就選中了中獎的那一門
這樣你換的話才會不中
然而,原PO的是3門,一開始選中的機率也有三份一(1/3)
從一開始你就選中也不是不可能的事
但就正如我上面說的
這是要解釋機率高低,不是憑直覺看彩數
就這樣,懂了嗎?
>>2184930
真正的電視遊戲主持人的確會這樣做
因為要保住大獎不能輕易送出
無題 無名 21/01/11(一)01:15:31 ID:1tA9tB0M No.2184953
無題 無名 21/01/11(一)01:29:50 ID:jDp94USQ No.2184955
>>2184949
因為這是數學問題,等同一些定理存在
不是你信不信的問題,你信不信對他正不正確存不存在根本沒影響
不會因為你不相信太陽從東方昇起,他就會從西方昇起的
就像你可以信神,但不可以用你信神來證明神的存在
反之你可以不信有鬼,但不可以用你不信有鬼來證明鬼不存在
你看法如何,信與不信也好,現實世界依然是按數學理論在運行
機率就是機率,就這樣簡單
所以我一開始就說你可以不信
真的
反正對世界沒影響,地球繼續會轉
因為這是數學問題,等同一些定理存在
不是你信不信的問題,你信不信對他正不正確存不存在根本沒影響
不會因為你不相信太陽從東方昇起,他就會從西方昇起的
就像你可以信神,但不可以用你信神來證明神的存在
反之你可以不信有鬼,但不可以用你不信有鬼來證明鬼不存在
你看法如何,信與不信也好,現實世界依然是按數學理論在運行
機率就是機率,就這樣簡單
所以我一開始就說你可以不信
真的
反正對世界沒影響,地球繼續會轉
無題 無名 21/01/11(一)01:35:40 ID:o/VLUZ6M No.2184958
>>2184949
>>但是66/100不等於2/3,就算約略2/3但也不是2/3
所以你根本不知道機率是什麼東西,跟你討論數學根本是白費唇舌
>>我要怎麼確認常規的數學理論和老王的理論(以及背書理論的理論)哪個是正確的?
我用算式去算每一百次都可以中六十次,重複實驗一千次都是如此
如果老王的夢可以一百次中一百次,重複實驗一千次也都呈現一樣的結果那我們就有理由去討論老王的夢是怎麼形成的,跟對結果有什麼關聯
但是沒有,結案.
>>天動說也可以正確的預測天體運行
不能
>>生醫領域的論文一大堆再現不出來
我們信任的是可以再現的,不能輕易再現的那只能叫做實驗跟紀錄而不能稱作論文
你貼的文章正好同意了這一點,裡面就說了為什麼一堆有前景的研究後面都會陷入膠著?
因為後面的實驗無法呈現前面的成果,表示中間有什麼不確定因素造成結論的不同
無法重複就不會穩定,沒有穩定就不能成為商品,當然就會陷入膠著
我們信任的是可以重複的結論,而非還在掙扎中的實驗
然是說因為某些實驗的不完整你就要去否定整個生物化學領域?
這就跟教會人覺得因為演化論中間有空白就認為神創論是對的一樣智障
科學跟數學從來不是因為我想,你想,或是我們想怎樣就怎樣
算式,結果,答案
什麼是什麼,就是什麼
>>為什麼我們可以認為現實世界是按數學理論在運行的?
請不要把有腦袋的一般人跟你相提並論
>>但是66/100不等於2/3,就算約略2/3但也不是2/3
所以你根本不知道機率是什麼東西,跟你討論數學根本是白費唇舌
>>我要怎麼確認常規的數學理論和老王的理論(以及背書理論的理論)哪個是正確的?
我用算式去算每一百次都可以中六十次,重複實驗一千次都是如此
如果老王的夢可以一百次中一百次,重複實驗一千次也都呈現一樣的結果那我們就有理由去討論老王的夢是怎麼形成的,跟對結果有什麼關聯
但是沒有,結案.
>>天動說也可以正確的預測天體運行
不能
>>生醫領域的論文一大堆再現不出來
我們信任的是可以再現的,不能輕易再現的那只能叫做實驗跟紀錄而不能稱作論文
你貼的文章正好同意了這一點,裡面就說了為什麼一堆有前景的研究後面都會陷入膠著?
因為後面的實驗無法呈現前面的成果,表示中間有什麼不確定因素造成結論的不同
無法重複就不會穩定,沒有穩定就不能成為商品,當然就會陷入膠著
我們信任的是可以重複的結論,而非還在掙扎中的實驗
然是說因為某些實驗的不完整你就要去否定整個生物化學領域?
這就跟教會人覺得因為演化論中間有空白就認為神創論是對的一樣智障
科學跟數學從來不是因為我想,你想,或是我們想怎樣就怎樣
算式,結果,答案
什麼是什麼,就是什麼
>>為什麼我們可以認為現實世界是按數學理論在運行的?
請不要把有腦袋的一般人跟你相提並論
>>2184959
>>天動說也可以正確的預測天體運行
>不能
其實在當年硬要凹的狀況下是可以靠畫出非常華麗的螺旋飛升天體運行軌跡來把模型硬套成符合天動說啦...
廣義來說也算是用天東說模型預測天體運行吧wwwwww
>>天動說也可以正確的預測天體運行
>不能
其實在當年硬要凹的狀況下是可以靠畫出非常華麗的螺旋飛升天體運行軌跡來把模型硬套成符合天動說啦...
廣義來說也算是用天東說模型預測天體運行吧wwwwww
無題 無名 21/01/11(一)01:43:36 ID:PRHvf.As No.2184961
>>2184960
唉從他去刁67%不等於2/3時我就覺得好像在跟13世紀的教會智障講話一樣....
唉從他去刁67%不等於2/3時我就覺得好像在跟13世紀的教會智障講話一樣....
>>2184959
>>但是66/100不等於2/3,就算約略2/3但也不是2/3
我只是要表達說「單靠實驗獲得的數據是無法證實理論的」
你永遠可以弄出一個更精確符合實驗數據的理論,但那個理論就可能跟天動說的圓周轉一樣,只是在錯的基礎上不斷逼近而已
>>我用算式去算每一百次都可以中六十次,重複實驗一千次都是如此
依照統計學來推斷會呈現以0.66為中心的正規分布,重複一千次多少會有幾次偏離0.66
不可能是100%準確
實驗上也會如此
但老王的夢與數學模型的預測不是0或1的差異,實驗觀察起來我們或許可以說數學模型效果比較好
但效果比較好就一定是真的嗎?
"The Copernican system was no more accurate than Ptolemy's system"*
至少在科卜勒改進系統之前,天動說是比較準確的學說
我們怎麼確定現有的數學就不是天動說,老王的夢就不是改進前的地動說呢?
另外就算可以穩定再現
會不會如牛頓力學一樣我們只是看到了簡潔的公式而忽略了難以觀測的細節
實際上牛頓力學只是狹義相對論在低速下的特例而已?
如果有人在18世紀就提出狹義相對論,絕對會被人拿著奧坎剃刀砍
*https://www.wikiwand.com/en/Geocentric_model
>>但是66/100不等於2/3,就算約略2/3但也不是2/3
我只是要表達說「單靠實驗獲得的數據是無法證實理論的」
你永遠可以弄出一個更精確符合實驗數據的理論,但那個理論就可能跟天動說的圓周轉一樣,只是在錯的基礎上不斷逼近而已
>>我用算式去算每一百次都可以中六十次,重複實驗一千次都是如此
依照統計學來推斷會呈現以0.66為中心的正規分布,重複一千次多少會有幾次偏離0.66
不可能是100%準確
實驗上也會如此
但老王的夢與數學模型的預測不是0或1的差異,實驗觀察起來我們或許可以說數學模型效果比較好
但效果比較好就一定是真的嗎?
"The Copernican system was no more accurate than Ptolemy's system"*
至少在科卜勒改進系統之前,天動說是比較準確的學說
我們怎麼確定現有的數學就不是天動說,老王的夢就不是改進前的地動說呢?
另外就算可以穩定再現
會不會如牛頓力學一樣我們只是看到了簡潔的公式而忽略了難以觀測的細節
實際上牛頓力學只是狹義相對論在低速下的特例而已?
如果有人在18世紀就提出狹義相對論,絕對會被人拿著奧坎剃刀砍
*https://www.wikiwand.com/en/Geocentric_model
>>2184968
>>單靠實驗獲得的數據是無法證實理論的
所以你不知道什麼叫做實驗什麼叫做理論
>>可能跟天動說的圓周轉一樣,只是在錯的基礎上不斷逼近而已
很顯然你也不知道天動說跟地動說的差距跟為什麼前者會被後者推翻
>>不可能是100%準確
所以你還是不了解什麼叫做機率
>>但效果比較好就一定是真的嗎?
更甚之你根本就沒有邏輯
講一大堆屁話也只是證明你就是個自大的笨蛋而已
你以為只有你正在進化嗎?
>>單靠實驗獲得的數據是無法證實理論的
所以你不知道什麼叫做實驗什麼叫做理論
>>可能跟天動說的圓周轉一樣,只是在錯的基礎上不斷逼近而已
很顯然你也不知道天動說跟地動說的差距跟為什麼前者會被後者推翻
>>不可能是100%準確
所以你還是不了解什麼叫做機率
>>但效果比較好就一定是真的嗎?
更甚之你根本就沒有邏輯
講一大堆屁話也只是證明你就是個自大的笨蛋而已
你以為只有你正在進化嗎?
無題 無名 21/01/11(一)02:29:53 ID:jDp94USQ No.2184973
無題 無名 21/01/11(一)02:42:02 ID:sgZX0eqY No.2184975
無題 無名 21/01/11(一)02:44:52 ID:/CVMYzO. No.2184976
>>2184949
原本我還打了一長串,結果發現閣下單純只是數學不好
一個以100為分母的分數有可能等於2/3嗎,笑死
不過連實驗數據的意義都不懂
看來閣下對科學的了解也不太多呢…
不過沒關係,就算是科學素養很爛的人
科學還是照樣會造福他們
讓他們仍然能上網發表些不科學的意見的
原本我還打了一長串,結果發現閣下單純只是數學不好
一個以100為分母的分數有可能等於2/3嗎,笑死
不過連實驗數據的意義都不懂
看來閣下對科學的了解也不太多呢…
不過沒關係,就算是科學素養很爛的人
科學還是照樣會造福他們
讓他們仍然能上網發表些不科學的意見的
>>2184969
我再幫忙從頭說明一次好了
規則
3扇門
當中有1中獎+2沒中獎
參與者選擇任一門後
主持人會在排除掉中獎門與被選中的前提下將門開只到只剩2扇未開
接著會詢問是否要換門
此時剩餘的兩扇門當中必有其中一扇是中獎門
若選擇不換則代表要一開始就選中
也就是有1/3的機率 因此換門中獎機率為2/3
將規模放大至100扇門後機率分別為1/100與99/100
第一次選擇 是從100扇門中挑一扇
而第二次選擇若換門則等同於一次開了另外的99扇門
我再幫忙從頭說明一次好了
規則
3扇門
當中有1中獎+2沒中獎
參與者選擇任一門後
主持人會在排除掉中獎門與被選中的前提下將門開只到只剩2扇未開
接著會詢問是否要換門
此時剩餘的兩扇門當中必有其中一扇是中獎門
若選擇不換則代表要一開始就選中
也就是有1/3的機率 因此換門中獎機率為2/3
將規模放大至100扇門後機率分別為1/100與99/100
第一次選擇 是從100扇門中挑一扇
而第二次選擇若換門則等同於一次開了另外的99扇門
>>2184964
那請拿sqrt(2)與-1顆蘋果給我
>>2184971
理論要正確除了吻合實驗結果外,也要符合既有邏輯
不然就如老王做夢一樣,要是他真的連續6次都給他夢到明牌矇到
你也不會認為老王的理論是正確的,因為他有可能第7次就猜不到了
而我就是要問「數學的邏輯,是否可以毫無顧忌的用在現實世界中?」
因為我並不知道「數學會一定符合現實」的根據
我只能藉由目前數學在自然科學上的表現說他很好用而已,但未來還能不能一樣好用我不知道
>>天動說跟地動說的差距跟為什麼前者會被後者推翻
‧科卜勒發現行星軌道是橢圓的
‧伽利略發現木星衛星
‧天動說無法解釋望遠鏡發明後觀察到的金星相(特別是這個)
‧牛頓發表萬有引力
https://www.wikiwand.com/en/Copernican_heliocentrism#/Copernican_Revolution
但這些都是後來才有的
在新證據出來之前既有的托勒密系統的逼近是比較準確的
所以我才會質疑就算是現行較精確的理論,也是有可能被未來的證據推翻的
而未來的事情我們並無法預測
那請拿sqrt(2)與-1顆蘋果給我
>>2184971
理論要正確除了吻合實驗結果外,也要符合既有邏輯
不然就如老王做夢一樣,要是他真的連續6次都給他夢到明牌矇到
你也不會認為老王的理論是正確的,因為他有可能第7次就猜不到了
而我就是要問「數學的邏輯,是否可以毫無顧忌的用在現實世界中?」
因為我並不知道「數學會一定符合現實」的根據
我只能藉由目前數學在自然科學上的表現說他很好用而已,但未來還能不能一樣好用我不知道
>>天動說跟地動說的差距跟為什麼前者會被後者推翻
‧科卜勒發現行星軌道是橢圓的
‧伽利略發現木星衛星
‧天動說無法解釋望遠鏡發明後觀察到的金星相(特別是這個)
‧牛頓發表萬有引力
https://www.wikiwand.com/en/Copernican_heliocentrism#/Copernican_Revolution
但這些都是後來才有的
在新證據出來之前既有的托勒密系統的逼近是比較準確的
所以我才會質疑就算是現行較精確的理論,也是有可能被未來的證據推翻的
而未來的事情我們並無法預測
無題 無名 21/01/11(一)03:29:34 ID:2DTc31OU No.2184989
>>2184993
第一扇門選定的當下 那扇門背後有中/沒中就已經是既定事實了
不會因為你所謂的換過去又換回來改變
那個機率就是1/總門數
換個比喻 箱子裡有100顆球 裡面有1顆中獎
你用右手隨便抓一顆 主持人把98顆沒中獎的拿走
箱中剩下的另一顆塞到你的左手
這時候問你要抽出左手或右手
你覺得你把左右手的球對調再對調之後 你右手的球會變顏色?
第一扇門選定的當下 那扇門背後有中/沒中就已經是既定事實了
不會因為你所謂的換過去又換回來改變
那個機率就是1/總門數
換個比喻 箱子裡有100顆球 裡面有1顆中獎
你用右手隨便抓一顆 主持人把98顆沒中獎的拿走
箱中剩下的另一顆塞到你的左手
這時候問你要抽出左手或右手
你覺得你把左右手的球對調再對調之後 你右手的球會變顏色?
>>2184995
每次這問題都會有人陷入奇怪的思考盲點......
麻煩請順著以下的說明思考
情境為100選1
1.一開始選擇的時候中獎率為?
>1/100
如果你的答案不是這個的話請說明為什麼
2.先選擇一扇門並排除掉98扇未中獎門後 此兩門背後是否一定有獎?
>是
如果不是的話請去把主持人抓出來打
3.那麼此兩扇門的中獎機率合計是否為1?
>是
如果不是的話請去把高中的機率統計看過一次
4.承1 一開始選擇的門中獎機率為1/100 那麼另一扇門的中獎機率是?
>99/100
題目3都問你合計是不是1了還能算錯的話再回頭去看前面謝謝
5.你的選擇有沒有能力改變門後的內容?
>沒有
這是數學問題禁止使用超能力謝謝
6.門後的東西沒有任何改變那麼機率會不會改變
>不會
會的話請提出 在條件不變下為什麼機率模型會變?
唯一一次造成機率模型變動的原因是
主持人在已知中獎為何門的前提下 抽掉了98扇"必定沒有中獎的門"
只要搞清楚條件機率到底是甚麼這題就不困難了
每次這問題都會有人陷入奇怪的思考盲點......
麻煩請順著以下的說明思考
情境為100選1
1.一開始選擇的時候中獎率為?
>1/100
如果你的答案不是這個的話請說明為什麼
2.先選擇一扇門並排除掉98扇未中獎門後 此兩門背後是否一定有獎?
>是
如果不是的話請去把主持人抓出來打
3.那麼此兩扇門的中獎機率合計是否為1?
>是
如果不是的話請去把高中的機率統計看過一次
4.承1 一開始選擇的門中獎機率為1/100 那麼另一扇門的中獎機率是?
>99/100
題目3都問你合計是不是1了還能算錯的話再回頭去看前面謝謝
5.你的選擇有沒有能力改變門後的內容?
>沒有
這是數學問題禁止使用超能力謝謝
6.門後的東西沒有任何改變那麼機率會不會改變
>不會
會的話請提出 在條件不變下為什麼機率模型會變?
唯一一次造成機率模型變動的原因是
主持人在已知中獎為何門的前提下 抽掉了98扇"必定沒有中獎的門"
只要搞清楚條件機率到底是甚麼這題就不困難了
>>2185000
>>主持人在已知中獎為何門的前提下 抽掉了98扇"必定沒有中獎的門"
你說到重點了,很多人都把分母擴大到100然後配用機率來告訴人「你不換就是N分之一,換了就是剩下的機率」
然而事實上到此為止是正確的邏輯,卻依然被這派的人偷藏概念「主持人把已知MISS的門開完剩下一個MISS與一個獎品」的條件;
光是最後一個這動作就打臉前面的「最大分母論」
>>主持人在已知中獎為何門的前提下 抽掉了98扇"必定沒有中獎的門"
你說到重點了,很多人都把分母擴大到100然後配用機率來告訴人「你不換就是N分之一,換了就是剩下的機率」
然而事實上到此為止是正確的邏輯,卻依然被這派的人偷藏概念「主持人把已知MISS的門開完剩下一個MISS與一個獎品」的條件;
光是最後一個這動作就打臉前面的「最大分母論」
>>2185009
有一個情境是換不換門機率一樣啦
第一次選完門之後
主持人在自己也不知道到底哪扇門有獎的前提下 隨意撤走98扇門
最後再問要不要換門
這時候不換門有1/100的機率中獎
換門也是1/100的機率中獎
剩下的98/100就是中獎的門早被撤走 換不換門都無所謂 反正都沒獎的機率wwwwwwww
有一個情境是換不換門機率一樣啦
第一次選完門之後
主持人在自己也不知道到底哪扇門有獎的前提下 隨意撤走98扇門
最後再問要不要換門
這時候不換門有1/100的機率中獎
換門也是1/100的機率中獎
剩下的98/100就是中獎的門早被撤走 換不換門都無所謂 反正都沒獎的機率wwwwwwww
>>2184870
>是2/3
不對 是1/2
你要看機率描述的對象
主持人開一扇門後再選
剩下兩扇所以"選到車"的機率是1/2沒錯
但是"換門選到車"的機率確實才是2/3
理解之後會覺得機率真的很機掰但卻又很合理
>是2/3
不對 是1/2
你要看機率描述的對象
主持人開一扇門後再選
剩下兩扇所以"選到車"的機率是1/2沒錯
但是"換門選到車"的機率確實才是2/3
理解之後會覺得機率真的很機掰但卻又很合理
>>2184977
你們別聽這個唬爛 實際上羊也是獎品
所以3扇門都有獎 你換不換中獎機率都是100%
跟現在抽卡遊戲的保底一樣 不過你抽到SSR車車機率是33.3333333X%
主持人把100%中獎的羊給你看了 剩下兩扇門也是100%中獎的
你們別聽這個唬爛 實際上羊也是獎品
所以3扇門都有獎 你換不換中獎機率都是100%
跟現在抽卡遊戲的保底一樣 不過你抽到SSR車車機率是33.3333333X%
主持人把100%中獎的羊給你看了 剩下兩扇門也是100%中獎的
>>2185027
所以就是國文不好不是數學不好
"換門這個動作選到車"的機率2/3才是你說的條件機率
"不換門選到車的機率"是1/3
至於剩下兩扇門 車在其中一扇的機率是1/2
這個恐怕大部分老師都不是這樣教所以你不懂不意外
你要看對機率描述的對象
所以就是國文不好不是數學不好
"換門這個動作選到車"的機率2/3才是你說的條件機率
"不換門選到車的機率"是1/3
至於剩下兩扇門 車在其中一扇的機率是1/2
這個恐怕大部分老師都不是這樣教所以你不懂不意外
你要看對機率描述的對象
>>2185028
>至於剩下兩扇門 車在其中一扇的機率是1/2
憑空迸出兩扇門 其中一扇有車一扇沒有
這樣的機率才是50/50
問題現在的狀況是
有一扇在3選1的一開始被選中的門
與
另一扇"在3選1後剩餘兩扇門中排除必定沒有車的一扇門後剩餘的一扇門"
對知曉整個流程的人來說機率是1/3跟2/3
如果前面步驟做了甚麼都不知道 給你兩扇門較你挑一扇 那才會是1/2
每次這題目想要傳遞點正確的小常識都要面對一堆鬼打牆真的讓人頭很痛...
>至於剩下兩扇門 車在其中一扇的機率是1/2
憑空迸出兩扇門 其中一扇有車一扇沒有
這樣的機率才是50/50
問題現在的狀況是
有一扇在3選1的一開始被選中的門
與
另一扇"在3選1後剩餘兩扇門中排除必定沒有車的一扇門後剩餘的一扇門"
對知曉整個流程的人來說機率是1/3跟2/3
如果前面步驟做了甚麼都不知道 給你兩扇門較你挑一扇 那才會是1/2
每次這題目想要傳遞點正確的小常識都要面對一堆鬼打牆真的讓人頭很痛...
>>2185030
你還是聽不懂= =
你要看對象
你舉的“知道不知道流程“跟我說的意思根本一樣
你真的是國文不好……
換不換門取到車
跟剩下兩扇門裡面哪個有車是不一樣的
換不換門因為加入了主持人幫你排除選項的變因
你換個說法說知不知道流程是一樣的意思
你還是聽不懂= =
你要看對象
你舉的“知道不知道流程“跟我說的意思根本一樣
你真的是國文不好……
換不換門取到車
跟剩下兩扇門裡面哪個有車是不一樣的
換不換門因為加入了主持人幫你排除選項的變因
你換個說法說知不知道流程是一樣的意思
無題 無名 21/01/11(一)09:44:54 ID:wyjYMHW. No.2185044
早上起床時想到一個更好理解的模型
A跟B在玩抽鬼牌
A手上沒牌 B手上有十張牌,其中一張為鬼牌
只要A抽中鬼牌就算A贏
遊戲開始(情境1)
A從B的牌中抽一張牌
直接翻開
請問A的勝率是?
遊戲開始(情境2)
A抽一張牌,直接翻開
如果A抽到的不是鬼牌,那B就翻開除了鬼牌之外的牌
翻開的牌部移除且依舊是B的手牌
並且詢問A要不要交換手牌(一開始選的一張牌換其他沒選的九張牌)
請問A應不應該作交換?為什麼?
遊戲開始(情境3)
A抽一張牌不翻開
B翻開除了鬼牌以外的牌,如果鬼牌被A抽走,那就保留一張牌不翻開
這時B再詢問A要不要交換手牌
請問A該不該交換手牌?為什麼?
請注意每次交換手牌都是拿A手上那一張牌去跟B的所有手牌作交換,翻開的牌不會被移除,而是繼續留在手牌上
A跟B在玩抽鬼牌
A手上沒牌 B手上有十張牌,其中一張為鬼牌
只要A抽中鬼牌就算A贏
遊戲開始(情境1)
A從B的牌中抽一張牌
直接翻開
請問A的勝率是?
遊戲開始(情境2)
A抽一張牌,直接翻開
如果A抽到的不是鬼牌,那B就翻開除了鬼牌之外的牌
翻開的牌部移除且依舊是B的手牌
並且詢問A要不要交換手牌(一開始選的一張牌換其他沒選的九張牌)
請問A應不應該作交換?為什麼?
遊戲開始(情境3)
A抽一張牌不翻開
B翻開除了鬼牌以外的牌,如果鬼牌被A抽走,那就保留一張牌不翻開
這時B再詢問A要不要交換手牌
請問A該不該交換手牌?為什麼?
請注意每次交換手牌都是拿A手上那一張牌去跟B的所有手牌作交換,翻開的牌不會被移除,而是繼續留在手牌上
無題 無名 21/01/11(一)09:48:47 ID:tWo.24y. No.2185045
其實認為不換沒差的原因是出於人性吧
邏輯推算很有道理
但是如果一開始就中了,換了變沒中=>
我真他媽的蠢
不換沒中=>
最多就是可惜但是不能算是蠢,畢竟一開始就沒中
總之理論上雖然換了機率比較高,但是為了不想承受一開始就選中換了沒中的風險,所以下意識的會認為不換才是比較好的,就算邏輯推理有道理也會認為那個不合理,作為心理安慰
邏輯推算很有道理
但是如果一開始就中了,換了變沒中=>
我真他媽的蠢
不換沒中=>
最多就是可惜但是不能算是蠢,畢竟一開始就沒中
總之理論上雖然換了機率比較高,但是為了不想承受一開始就選中換了沒中的風險,所以下意識的會認為不換才是比較好的,就算邏輯推理有道理也會認為那個不合理,作為心理安慰
無題 無名 21/01/11(一)09:50:52 ID:F1BBr7tY No.2185046
無題 主持人的手大概會開門開到脫臼... 21/01/11(一)10:28:35 ID:T1TO/ooQ No.2185057
我們就不用1000扇門來解釋,試試用1000人來解釋看看
<壹>不換門的對照組:
1000人各自在3道門中選一道門,此時大約會有333人中車,其餘667人中羊。
若主持人把這3000道門中的1000道槓龜門打開,且1000人不換選擇,中獎人理所當然約有333人
由此得知機率約1/3
<貳>換門的對照組:
1000人各自在3道門中選1道門,此時大約會有333人中車,其餘667人中羊。
若主持人把這3000道門中的1000道槓龜門打開,在這個時間點,剩餘的2000道門中:
原本被1000人選取的1000道門中,約333道門後有車,其餘667道門後有羊。
而剩下沒被選取的1000道門中,約667道門後有羊,其餘333道門後有車。
維持原選擇的話,結果同<壹>。1000人都換門的話,667人中車,剩下中羊
由此得知機率約2/3
<壹>不換門的對照組:
1000人各自在3道門中選一道門,此時大約會有333人中車,其餘667人中羊。
若主持人把這3000道門中的1000道槓龜門打開,且1000人不換選擇,中獎人理所當然約有333人
由此得知機率約1/3
<貳>換門的對照組:
1000人各自在3道門中選1道門,此時大約會有333人中車,其餘667人中羊。
若主持人把這3000道門中的1000道槓龜門打開,在這個時間點,剩餘的2000道門中:
原本被1000人選取的1000道門中,約333道門後有車,其餘667道門後有羊。
而剩下沒被選取的1000道門中,約667道門後有羊,其餘333道門後有車。
維持原選擇的話,結果同<壹>。1000人都換門的話,667人中車,剩下中羊
由此得知機率約2/3
無題 無名 21/01/11(一)10:30:40 ID:kQV57dhw No.2185058
>>2185056
又一個來添亂的......
為什麼你8次裡面可以選到4次a
想清楚再重新寫一次謝謝
又一個來添亂的......
為什麼你8次裡面可以選到4次a
想清楚再重新寫一次謝謝
無題 無名 21/01/11(一)10:37:14 ID:qag32I4I No.2185061
>>2185056
> 主持人去掉哪一只羊是不可知的
那你他媽的就不能把2和4寫出來 白痴
> 主持人去掉哪一只羊是不可知的
那你他媽的就不能把2和4寫出來 白痴
無題 無名 21/01/11(一)10:39:38 ID:km7OWrms No.2185063
盲點就是主持人知道答案而且他只會開垃圾門
無題 無名 21/01/11(一)10:42:46 ID:yeIal6o. No.2185065
無題 無名 21/01/11(一)10:44:16 ID:qag32I4I No.2185066
>>2185056
有abc三門a有車 b有羊 c有羊
1第一次選a門主持人去掉羊不換門仍選a
2第一次選a門主持人去掉羊,換門改選另一扇
3第一次選b門主持人去掉羊不換門仍選b
4第一次選b門主持人去掉羊,換門改選另一扇
5第一次選c門主持人去掉羊不換門仍選c
6第一次選c門主持人去掉羊,換門改選另一扇
換門選車:2種,換門選羊:1種
所以換門中獎機率=2/(2+1)=2/3
不換門選車:1種,不換門選羊:2種
所以不換門中獎機率=1/(1+2)=1/3
有abc三門a有車 b有羊 c有羊
1第一次選a門主持人去掉羊不換門仍選a
2第一次選a門主持人去掉羊,換門改選另一扇
3第一次選b門主持人去掉羊不換門仍選b
4第一次選b門主持人去掉羊,換門改選另一扇
5第一次選c門主持人去掉羊不換門仍選c
6第一次選c門主持人去掉羊,換門改選另一扇
換門選車:2種,換門選羊:1種
所以換門中獎機率=2/(2+1)=2/3
不換門選車:1種,不換門選羊:2種
所以不換門中獎機率=1/(1+2)=1/3
無題 無名 21/01/11(一)10:45:28 ID:/uEEN.PU No.2185068
>>2185056
>不換門選車機率2/8
三扇門蝦七八亂猜都有1/3機率會中
你居然還可以自己降成1/4
>不換門選車機率2/8
三扇門蝦七八亂猜都有1/3機率會中
你居然還可以自己降成1/4
我比較想要山羊
羊肉爐
羊肉爐
無題 無名 21/01/11(一)11:24:49 ID:yeIal6o. No.2185071
>>2185070
但把車賣掉換來的錢可以買1000鍋羊肉爐還有找
但把車賣掉換來的錢可以買1000鍋羊肉爐還有找
>>2184949
你的結尾在每段論述是一樣的,雖然你很認真想討論,但其實不是討論數學。
如同你說我們的每次理論與數據都有可能是在錯誤的基礎上疊加,感覺不少哲學家們為此也杞憂了數千年。
只是我們的生命極度有限,所以我個人是認為除非實力高到能誕生新理論,否則在現有規則下生活不會有甚麼巨變。
(除非這麼剛好我們這代碰上了電影中那種會導致生活環境大改的理論崩壞)
不然跟著現有基礎生活沒太大不好。
你想討論理論,但其實也是想幫自己得證。
你的結尾在每段論述是一樣的,雖然你很認真想討論,但其實不是討論數學。
如同你說我們的每次理論與數據都有可能是在錯誤的基礎上疊加,感覺不少哲學家們為此也杞憂了數千年。
只是我們的生命極度有限,所以我個人是認為除非實力高到能誕生新理論,否則在現有規則下生活不會有甚麼巨變。
(除非這麼剛好我們這代碰上了電影中那種會導致生活環境大改的理論崩壞)
不然跟著現有基礎生活沒太大不好。
你想討論理論,但其實也是想幫自己得證。
無題 無名 21/01/11(一)11:35:35 ID:xDAEuZaM No.2185076
>>2185041
私立維多利亞雙語中學,小三還會教肛交
私立維多利亞雙語中學,小三還會教肛交
無題 無名 21/01/11(一)12:25:39 ID:slN9wIpU No.2185102
我剛問我威力彩簽中的朋友
他說這問題換不換都沒差
他隨便都中大獎
他說這問題換不換都沒差
他隨便都中大獎
>>2185073
看著2000年前對於地平說的概念
看著1000年前對於帝制/君主制的概念
看著100年前對於電腦/宇宙的概念
看著30年對著智慧型手機/平板的概念
看著10年前對VR的概念
以前的哲學不過是理想而已~ 在餓著肚子情況下想的
現在的哲學不過是吃飽太閒~ 在沒事幹的情況想的
如果單純用本串來討論
因為主持人一定會打開一個(或更多個)不會中的門
選項由原本的1/3(或更多分母)的機率提高為變成1/2而已
跟選不選~ 換不換無關
看著2000年前對於地平說的概念
看著1000年前對於帝制/君主制的概念
看著100年前對於電腦/宇宙的概念
看著30年對著智慧型手機/平板的概念
看著10年前對VR的概念
以前的哲學不過是理想而已~ 在餓著肚子情況下想的
現在的哲學不過是吃飽太閒~ 在沒事幹的情況想的
如果單純用本串來討論
因為主持人一定會打開一個(或更多個)不會中的門
選項由原本的1/3(或更多分母)的機率提高為變成1/2而已
跟選不選~ 換不換無關
無題 傻逼 21/01/11(一)12:59:59 ID:DTXqF9mY No.2185117
呵呵哈哈哈哈哈哈
話說"意願"這種東西是不是不能用機率來講啊...?
你又不是丟銅板決定
你又不是丟銅板決定
無題 無名 21/01/11(一)13:02:20 ID:wyjYMHW. No.2185120
無題 無名 21/01/11(一)13:14:01 ID:jDp94USQ No.2185124
無題 無名 21/01/11(一)13:27:09 ID:jDp94USQ No.2185126
無題 無名 21/01/11(一)13:40:33 ID:jDp94USQ No.2185129
>>2184982
對
未來的事情我們並無法預測
所以你也不可能預測到,未來哪一些精確的理論會被推翻
你不相信現今的理論的話,也必先找到現今理論不可信的點
然後找個更為可信的,足以推翻原理論的新理論出來才行
找到能說服眾人的理據,理論才能改變
連證據都沒有,憑什麼會比一個受學界公認的理論更可信
現行較精確的理論,有可能被未來的證據推翻,並不是現今理論不可信的『確實證據』,這只是你個人毫無根據的妄想而已
如果你不相信現今的理論,請先找『確實證據』來推翻他
不然說什麼,都只是你個人痴人說夢而已
對
未來的事情我們並無法預測
所以你也不可能預測到,未來哪一些精確的理論會被推翻
你不相信現今的理論的話,也必先找到現今理論不可信的點
然後找個更為可信的,足以推翻原理論的新理論出來才行
找到能說服眾人的理據,理論才能改變
連證據都沒有,憑什麼會比一個受學界公認的理論更可信
現行較精確的理論,有可能被未來的證據推翻,並不是現今理論不可信的『確實證據』,這只是你個人毫無根據的妄想而已
如果你不相信現今的理論,請先找『確實證據』來推翻他
不然說什麼,都只是你個人痴人說夢而已
https://docs.google.com/spreadsheets/d/1z9RquM658qW5NUzJ9T73ASI2DM_AmTMhbICLvTgzNa8/edit?usp=sharing
無題 無名 21/01/11(一)15:31:54 ID:YVh/776A No.2185148
>>2185138
>不換門得車1/6
就跟你說三扇門閉著眼睛亂猜也有1/3會中了
>不換門得車1/6
就跟你說三扇門閉著眼睛亂猜也有1/3會中了
>>2185138
其實我一直有個迷思
假設某個人是從節目播出到一半時才看
也就是主持人開啟其中一扇門後才開始看
他猜中車子的機率很理所當然的是1/2
那為什麼答題者和這個人會有如此差異?
並非不相信一般看到的解答
只是如果一個答案無法從多方面驗證,便無法確定它是正確的
不過看了你的內容我大概理解為什麼會有此差別
多數人的看法並非是直覺或常識錯誤
而是對題目本身的理解錯誤
還有,主持人開門之後,對答題者來說猜中車子的機率其實也同樣是1/2
會造成差異是在題目的論述上
其實我一直有個迷思
假設某個人是從節目播出到一半時才看
也就是主持人開啟其中一扇門後才開始看
他猜中車子的機率很理所當然的是1/2
那為什麼答題者和這個人會有如此差異?
並非不相信一般看到的解答
只是如果一個答案無法從多方面驗證,便無法確定它是正確的
不過看了你的內容我大概理解為什麼會有此差別
多數人的看法並非是直覺或常識錯誤
而是對題目本身的理解錯誤
還有,主持人開門之後,對答題者來說猜中車子的機率其實也同樣是1/2
會造成差異是在題目的論述上
無題 無名 21/01/11(一)17:50:38 ID:Wf094SrI No.2185188
>>2185186
因為有些扯1/2是在扯自己願不願意換.....
因為有些扯1/2是在扯自己願不願意換.....
無題 無名 21/01/11(一)18:00:34 ID:Pa.ZRaQw No.2185194
>>2184839
>我憑什麼要相信一連串抽象的數字,而不是顯而易見的常識?
>我怎麼能相信現實世界會照著你說的機率理論運作?
那你FGO可以不要抽PickUP池 就抽一般大雜池阿
反正機率提升是一連串抽象的數字
>我憑什麼要相信一連串抽象的數字,而不是顯而易見的常識?
>我怎麼能相信現實世界會照著你說的機率理論運作?
那你FGO可以不要抽PickUP池 就抽一般大雜池阿
反正機率提升是一連串抽象的數字
>>2185150
>>假設某個人是從節目播出到一半時才看
>>那為什麼答題者和這個人會有如此差異?
我的媽呀,不要在想這種奇怪的問題了
猜中車的機率會變成1/2只會是在本來就只有兩扇門的狀況之下,這又不是量子力學觀測者的介入與否會造成觀測結果的改變
三門問題就是一整個連續事件你不能拆開來看待,因為你一開始就選了一扇門了!如果最後的機率是1/2就沒有辦法回推到最初狀況,因為那代表題目的答案只會有兩種結果,但是三門問題最後會有三種(見附圖)
>>多數人的看法並非是直覺或常識錯誤
事實上就是!這個問題當初在學界掀起一陣風潮就是因為它的答案"違反直覺",但是數學並不是基於常識或是直覺去計算
而且老實說人類的常識跟直覺長期來看並不可靠,因為都不是基於理解而是經驗,錯誤的嘗試跟直覺其實就是迷信
你總不會說迷信是對的嗎?
>>假設某個人是從節目播出到一半時才看
>>那為什麼答題者和這個人會有如此差異?
我的媽呀,不要在想這種奇怪的問題了
猜中車的機率會變成1/2只會是在本來就只有兩扇門的狀況之下,這又不是量子力學觀測者的介入與否會造成觀測結果的改變
三門問題就是一整個連續事件你不能拆開來看待,因為你一開始就選了一扇門了!如果最後的機率是1/2就沒有辦法回推到最初狀況,因為那代表題目的答案只會有兩種結果,但是三門問題最後會有三種(見附圖)
>>多數人的看法並非是直覺或常識錯誤
事實上就是!這個問題當初在學界掀起一陣風潮就是因為它的答案"違反直覺",但是數學並不是基於常識或是直覺去計算
而且老實說人類的常識跟直覺長期來看並不可靠,因為都不是基於理解而是經驗,錯誤的嘗試跟直覺其實就是迷信
你總不會說迷信是對的嗎?
無題 無名 21/01/11(一)18:12:11 ID:Pa.ZRaQw No.2185200
>>2184879
>搞不好我1/3就猜對了 換了不就什麼都沒了
其實就跟打麻將一樣
如果你起手就聽單吊2萬,結果進一張牌你可以轉聽1/4萬
這時你會轉章聽 還是繼續單吊?
機率上1/4萬對倒胡兩張比較有利 但你也有可能下一張牌馬上就摸到二萬 如果換了就沒了
你可以相信你的強運 但你不能否認1/4萬對倒的胡牌機率比單吊2萬高 端看你個人選擇相信運氣還是機率
>搞不好我1/3就猜對了 換了不就什麼都沒了
其實就跟打麻將一樣
如果你起手就聽單吊2萬,結果進一張牌你可以轉聽1/4萬
這時你會轉章聽 還是繼續單吊?
機率上1/4萬對倒胡兩張比較有利 但你也有可能下一張牌馬上就摸到二萬 如果換了就沒了
你可以相信你的強運 但你不能否認1/4萬對倒的胡牌機率比單吊2萬高 端看你個人選擇相信運氣還是機率
>>2185197
思考才會進步
我反而覺得沒想過這問題才是一廂情願接受答案沒去理解
不過確實如你所說,這不是獨立事件
倘若只論「猜中」,那是獨立事件,所以機率是1/2
然而「換門」是連續事件,因為一開始就選過門了
我會說並非直覺或常識錯誤,是因為多數人沒能理解「換門」不是獨立事件
思考才會進步
我反而覺得沒想過這問題才是一廂情願接受答案沒去理解
不過確實如你所說,這不是獨立事件
倘若只論「猜中」,那是獨立事件,所以機率是1/2
然而「換門」是連續事件,因為一開始就選過門了
我會說並非直覺或常識錯誤,是因為多數人沒能理解「換門」不是獨立事件
你有1/3的機會中車,2/3的機會中羊
假設你的第一次中車(1/3):你換門必中羊
假設你的第一次中羊(2/3):你換門必中車
不換門的情況下:
假設你的第一次中車(1/3):不換門必中車
假設你的第一次中羊(2/3):不換門必中羊
一百道門並踢開九十八道羊的門的情況下:
假設你的第一次中車(1/100):換門中羊
假設你的第一次中羊(99/100):換門中車
一萬道門,踢開9998道羊的情況:
假設你的第一次中車(1/10000):換門中羊
假設你的第一次中羊(9999/10000):換門中車
百萬道門,踢開999998道羊的情況:
假設你的第一次中車(1/1000000):換門中羊
假設你的第一次中羊(9999/1000000):換門中車
主持人表示腳痛
假設你的第一次中車(1/3):你換門必中羊
假設你的第一次中羊(2/3):你換門必中車
不換門的情況下:
假設你的第一次中車(1/3):不換門必中車
假設你的第一次中羊(2/3):不換門必中羊
一百道門並踢開九十八道羊的門的情況下:
假設你的第一次中車(1/100):換門中羊
假設你的第一次中羊(99/100):換門中車
一萬道門,踢開9998道羊的情況:
假設你的第一次中車(1/10000):換門中羊
假設你的第一次中羊(9999/10000):換門中車
百萬道門,踢開999998道羊的情況:
假設你的第一次中車(1/1000000):換門中羊
假設你的第一次中羊(9999/1000000):換門中車
主持人表示腳痛
無題 無名 21/01/11(一)18:22:47 ID:nrxw.egg No.2185204
>>2185201
你那不叫思考那叫鬼打牆,代表你一開始就沒有理解過機率跟三門問題
這個鬼東西最早可以追溯到1889,在1975被廣泛討論,在1990被解出後又掀起一陣風潮,甚至還有變體的三囚問題
去思考牛為什麼會是牛並不是進步好嗎?
>>倘若只論「猜中」
就算只論猜中也不會是1/2機率,因為一開始有他媽的三扇門啊!
看附圖啦!
你那不叫思考那叫鬼打牆,代表你一開始就沒有理解過機率跟三門問題
這個鬼東西最早可以追溯到1889,在1975被廣泛討論,在1990被解出後又掀起一陣風潮,甚至還有變體的三囚問題
去思考牛為什麼會是牛並不是進步好嗎?
>>倘若只論「猜中」
就算只論猜中也不會是1/2機率,因為一開始有他媽的三扇門啊!
看附圖啦!
無題 無名 21/01/11(一)18:27:44 ID:PRHvf.As No.2185206
>>2185203
今天你買了一張大樂透,與其他2300萬-1人一樣都人手一張
突然,有個樂透公司的內部員工說其實開獎是預錄好的,已經排除了2300萬-2人的非頭獎中獎彩票,剩下你與另外一個疑似頭獎得主的彩票,但只有一張是頭獎,另一張是垃圾彩票,故意弔你們胃口
此刻,對方聯繫你問你要不要交換,你要換嗎?
今天你買了一張大樂透,與其他2300萬-1人一樣都人手一張
突然,有個樂透公司的內部員工說其實開獎是預錄好的,已經排除了2300萬-2人的非頭獎中獎彩票,剩下你與另外一個疑似頭獎得主的彩票,但只有一張是頭獎,另一張是垃圾彩票,故意弔你們胃口
此刻,對方聯繫你問你要不要交換,你要換嗎?
>>2185150
你要說差異在題目的論述上也沒錯 但更正確的說法是擁有的資訊不同
在你提出的情境中有三種不同的機率模型
1.從頭到尾參與活動者
典型的1/3與2/3
2.只知道兩扇門後面其中一扇是中獎的吃瓜群眾
你提到的1/2與1/2
3.從一開始就知道答案的主持人
沒有甚麼機率了 就很單純的1與0
明明是同樣的兩扇門 為什麼可以得出截然不同的三種結論?
就是因為三者所擁有個資訊不同
因此機率雖然可以幫你更接近真實 但同時你也要有足夠的資訊提供計算判斷
這就是為什麼一直提到"條件"機率的關係
你要說差異在題目的論述上也沒錯 但更正確的說法是擁有的資訊不同
在你提出的情境中有三種不同的機率模型
1.從頭到尾參與活動者
典型的1/3與2/3
2.只知道兩扇門後面其中一扇是中獎的吃瓜群眾
你提到的1/2與1/2
3.從一開始就知道答案的主持人
沒有甚麼機率了 就很單純的1與0
明明是同樣的兩扇門 為什麼可以得出截然不同的三種結論?
就是因為三者所擁有個資訊不同
因此機率雖然可以幫你更接近真實 但同時你也要有足夠的資訊提供計算判斷
這就是為什麼一直提到"條件"機率的關係
>>2185205
很早出現又怎樣?
你第一次遇到這問題就答對嗎?
答錯了有想過自己的答案和正確答案為什麼不一樣嗎?
還是只是純粹接受正確答案是如此?
並非創造出新東西才叫進步
個人的進步才會帶動社會進步
哪怕你再天才也是靠前人的堆疊加上自己思考才能創新
平常沒養成思考習慣真的遇到問題也會空轉
很早出現又怎樣?
你第一次遇到這問題就答對嗎?
答錯了有想過自己的答案和正確答案為什麼不一樣嗎?
還是只是純粹接受正確答案是如此?
並非創造出新東西才叫進步
個人的進步才會帶動社會進步
哪怕你再天才也是靠前人的堆疊加上自己思考才能創新
平常沒養成思考習慣真的遇到問題也會空轉
這麼無聊的問題可以討論這麼久喔
其實也沒什麼
會在那扯換門中獎機率高的原因很簡單
你們忘了這是一個節目
節目當然要控制時間長短
所以主持人會一直問你要不要換拖延時間
最多會拖延到1/2 如此而已
看起來好像就比較高機率中獎了
但正常狀況
只要內部沒有偷換中獎位置的話
中獎機率就是1/3不會改變
這可不是薛丁格的貓箱實驗好嗎
不會因為觀測改變事實
前提是內部沒有人去動手腳
但節目效果來講
當然就會把機率控制到1/2達到節目收視高潮
並且拖延節目時間內容不足的問題罷了
其實也沒什麼
會在那扯換門中獎機率高的原因很簡單
你們忘了這是一個節目
節目當然要控制時間長短
所以主持人會一直問你要不要換拖延時間
最多會拖延到1/2 如此而已
看起來好像就比較高機率中獎了
但正常狀況
只要內部沒有偷換中獎位置的話
中獎機率就是1/3不會改變
這可不是薛丁格的貓箱實驗好嗎
不會因為觀測改變事實
前提是內部沒有人去動手腳
但節目效果來講
當然就會把機率控制到1/2達到節目收視高潮
並且拖延節目時間內容不足的問題罷了
無題 無名 21/01/11(一)18:43:19 ID:kQV57dhw No.2185213
無題 無名 21/01/11(一)18:51:24 ID:nrxw.egg No.2185217
>>2185207
突然發現我的ID有egg
突然發現我的ID有egg
>>2185210
你以為過去數十年你是第一個想到這個問題的嗎?北七!
>>答錯了有想過自己的答案和正確答案為什麼不一樣嗎?
蔣幹化,就講過幾百遍了這個問題為什麼會這麼知名就是因為最後的答案違反直覺阿幹!除了那個天才女之外一般人都是答錯的啦!
整個三門問題跟解答就是世代堆疊下來才成為經典的,就是用過各種不同的想法去論證才會如此有趣
>>只是純粹接受正確答案是如此?
只是純粹去質疑正確答案不叫進步,那叫憤世忌俗
講了一堆跟題目無關的屁話我也沒看到你們有提出多少建設性的意見或是算式出來啊?
你以為過去數十年你是第一個想到這個問題的嗎?北七!
>>答錯了有想過自己的答案和正確答案為什麼不一樣嗎?
蔣幹化,就講過幾百遍了這個問題為什麼會這麼知名就是因為最後的答案違反直覺阿幹!除了那個天才女之外一般人都是答錯的啦!
整個三門問題跟解答就是世代堆疊下來才成為經典的,就是用過各種不同的想法去論證才會如此有趣
>>只是純粹接受正確答案是如此?
只是純粹去質疑正確答案不叫進步,那叫憤世忌俗
講了一堆跟題目無關的屁話我也沒看到你們有提出多少建設性的意見或是算式出來啊?
無題 無名 21/01/11(一)19:05:52 ID:nZVLQLYs No.2185222
無題 無名 21/01/11(一)19:24:31 ID:kXbcC1Tw No.2185224
事件:歡樂惡搞經典三門
出現頻率:半年至一年
事件內容:
討論三門問題時必定會有
1.主目標不斷跳針鬼打牆(可能是哲學系或夜校數學系)
2.熱心島民各種解釋跟論證
3.其他數學白癡或哲學精障自己跳出來提出莫名其妙的機率跟論點
4.回應過多沉串,不懂的下次還是一樣跳出來搶當主目標
出現頻率:半年至一年
事件內容:
討論三門問題時必定會有
1.主目標不斷跳針鬼打牆(可能是哲學系或夜校數學系)
2.熱心島民各種解釋跟論證
3.其他數學白癡或哲學精障自己跳出來提出莫名其妙的機率跟論點
4.回應過多沉串,不懂的下次還是一樣跳出來搶當主目標
>>2185216
>為什麼機率還會隨時間改變啦
所以就是到現在還一堆人一知半解
我上面就說了
你要搞清楚機率描述的對象
看起來很多人就是搞不清楚對象結果都混在一起講了
上面解釋一長串都沒有必要
搞清楚是在講"換門會中"的機率
還是"車在某扇門裡"的機率
>為什麼機率還會隨時間改變啦
所以就是到現在還一堆人一知半解
我上面就說了
你要搞清楚機率描述的對象
看起來很多人就是搞不清楚對象結果都混在一起講了
上面解釋一長串都沒有必要
搞清楚是在講"換門會中"的機率
還是"車在某扇門裡"的機率
無題 無名 21/01/11(一)19:32:56 ID:RSA9QZZ2 No.2185226
無題 無名 21/01/11(一)19:51:00 ID:nZVLQLYs No.2185232
>>2185225
你這麼說就很清楚了
不過我覺得多數人用n扇門n-1羊1車,選1又抽掉n-2扇有羊的門這例子好像不太適合
感覺換成選1又抽掉1扇門比較好理解問題在哪
畢竟前者換與不換能直接體現在結果上,不中的換了會中,會中的換了不中
而後者不中的換了會中的機率則是1/(n-2),n扇門減掉自選&開啟的門之後,只有1扇門會中
你這麼說就很清楚了
不過我覺得多數人用n扇門n-1羊1車,選1又抽掉n-2扇有羊的門這例子好像不太適合
感覺換成選1又抽掉1扇門比較好理解問題在哪
畢竟前者換與不換能直接體現在結果上,不中的換了會中,會中的換了不中
而後者不中的換了會中的機率則是1/(n-2),n扇門減掉自選&開啟的門之後,只有1扇門會中
這大概是我在島上看過第三次的蒙提霍爾問題
每次都有人堅持是1/2
維基百科都寫得清清楚楚
還能講出一堆狗屁道理
笑死
每次都有人堅持是1/2
維基百科都寫得清清楚楚
還能講出一堆狗屁道理
笑死
>>2185216
ABCD四個好了 假設A中獎 你選BCD
問你要不要換就是讓你去改選門
不然直接開A 直接回合結束 byebye 下一位
你改選A之後 他按照順序問你換不換並打開BCD的門
因為A你已經換過了 他可以不再問A要不要換 只需要把後面的門慢慢開掉 就會變成1/2了
跟你講障眼法 你大概也聽不懂吧 唉
你還是快去讀書或工作吧
ABCD四個好了 假設A中獎 你選BCD
問你要不要換就是讓你去改選門
不然直接開A 直接回合結束 byebye 下一位
你改選A之後 他按照順序問你換不換並打開BCD的門
因為A你已經換過了 他可以不再問A要不要換 只需要把後面的門慢慢開掉 就會變成1/2了
跟你講障眼法 你大概也聽不懂吧 唉
你還是快去讀書或工作吧
>>2185240
你玩的這個到底是哪一國的遊戲又跟這一串有個屁關係,真的就如你所說的我完全沒看懂
你玩的這個到底是哪一國的遊戲又跟這一串有個屁關係,真的就如你所說的我完全沒看懂
>>2185243
所以你是2p還1p拉 角色定為一下好嗎 一直換id耶你
所以你是2p還1p拉 角色定為一下好嗎 一直換id耶你
無題 無名 21/01/11(一)20:25:23 ID:kQV57dhw No.2185247
無題 無名 21/01/11(一)20:25:26 ID:EcFEqVOU No.2185248
無題 無名 21/01/11(一)20:26:56 ID:2l5xL6Oc No.2185250
無題 無名 21/01/11(一)20:28:45 ID:ivMAnPbw No.2185251
無題 無名 21/01/11(一)20:31:36 ID:bKzQSStU No.2185252
>>2185233
搞清楚機率描述什麼就不會弄錯
1.一開始門三選一機率1/3
2.主持人刪去後,換門會中獎的機率2/3
3.主持人刪去後,兩扇門其中一扇有車的機率1/2
會認為1/2的八成都是以3的角度在解讀
搞清楚機率描述什麼就不會弄錯
1.一開始門三選一機率1/3
2.主持人刪去後,換門會中獎的機率2/3
3.主持人刪去後,兩扇門其中一扇有車的機率1/2
會認為1/2的八成都是以3的角度在解讀
無題 無名 21/01/11(一)20:51:47 ID:ed6UYMbo No.2185263
無題 無名 21/01/11(一)20:53:22 ID:wyjYMHW. No.2185264
影片沒錯 但是現實通常三個山羊
電視台現在就4黑心
電視台現在就4黑心
無題 無名 21/01/11(一)21:09:07 ID:nrxw.egg No.2185268
>>2185265
或是一台小模型車
或是一台小模型車
無題 無名 21/01/11(一)21:11:28 ID:Pa.ZRaQw No.2185270
我覺得大家都解釋得太細緻了 讓一堆閱讀障礙者懶得看繼續跳針
這種系列的問題都是因為差距不大 讓人被常識誤導了
其實把差距拉大就容易懂了 剩下的就自己思考
假設今天題目是10扇門 你一樣先選一扇門 然後主持人一樣會開掉其餘8扇有羊的門 讓場上只剩兩扇門
這種情況下 你還會堅持不換你原本用1/10的機率去選的門嗎?
這種系列的問題都是因為差距不大 讓人被常識誤導了
其實把差距拉大就容易懂了 剩下的就自己思考
假設今天題目是10扇門 你一樣先選一扇門 然後主持人一樣會開掉其餘8扇有羊的門 讓場上只剩兩扇門
這種情況下 你還會堅持不換你原本用1/10的機率去選的門嗎?
無題 無名 21/01/11(一)21:14:04 ID:kQV57dhw No.2185271
無題 無名 21/01/11(一)21:16:33 ID:wyjYMHW. No.2185272
仔細想一想
山羊跟車子不對等的地方在哪裡
開門如果開到山羊-->助手小姐把山羊牽出門給參賽者
開門如果開到車子-->主持人會給參賽者車鑰匙
那麼~~三道門後面應該都是山羊
主持人開掉一個門~參賽者開掉一扇門之後
助手小姐悄悄地把鏡子放在第三扇門的山羊前面
結局開門時
就可以透過鏡子看到第四扇門後面的車子了
山羊跟車子不對等的地方在哪裡
開門如果開到山羊-->助手小姐把山羊牽出門給參賽者
開門如果開到車子-->主持人會給參賽者車鑰匙
那麼~~三道門後面應該都是山羊
主持人開掉一個門~參賽者開掉一扇門之後
助手小姐悄悄地把鏡子放在第三扇門的山羊前面
結局開門時
就可以透過鏡子看到第四扇門後面的車子了
無題 無名 21/01/11(一)21:20:34 ID:nrxw.egg No.2185276
>>2185270
簡單來說,兩種可能
1.我天生神力,一選就中,根本就不需要換
2.我運氣不好,選錯了,但主持人給了我機會換成正確的選項
在門越多的狀態下,2的機率會增加,因為你第一次天生神力就中的機會會越小,在趨近無限道門的狀態下,甚至只要隨便開一道,換門幾乎都會中
簡單來說,兩種可能
1.我天生神力,一選就中,根本就不需要換
2.我運氣不好,選錯了,但主持人給了我機會換成正確的選項
在門越多的狀態下,2的機率會增加,因為你第一次天生神力就中的機會會越小,在趨近無限道門的狀態下,甚至只要隨便開一道,換門幾乎都會中
無題 無名 21/01/11(一)21:21:20 ID:Tg1Uf.56 No.2185278
>>2185274
你再給我亂一次試試看
你再給我亂一次試試看
>ID:wyjYMHW.
小心暴怒廚出沒
暴怒廚常有的特徵
易怒
跳針
自我中心
代溝嚴重
通常很智障
看到請無視並且別回應他
小心暴怒廚出沒
暴怒廚常有的特徵
易怒
跳針
自我中心
代溝嚴重
通常很智障
看到請無視並且別回應他
無題 無名 21/01/11(一)21:27:34 ID:ed6UYMbo No.2185282
>ID:wyjYMHW.
小心暴怒廚出沒
暴怒廚常有的特徵
易怒
跳針
自我中心
代溝嚴重
通常很智障
看到請無視並且別回應他
補充
少了一點
缺乏幽默感
通常就是很自以為並且病態的認真還有些情緒不穩的現象
因此非常容易暴怒w
小心暴怒廚出沒
暴怒廚常有的特徵
易怒
跳針
自我中心
代溝嚴重
通常很智障
看到請無視並且別回應他
補充
少了一點
缺乏幽默感
通常就是很自以為並且病態的認真還有些情緒不穩的現象
因此非常容易暴怒w
>>2185270
其實我不太理解為什麼這樣會比較容易懂
會認為是1/2的思路是「認為只剩2扇門,2選1就是1/2」
這種說明方式結果還是剩2扇門啊
應該要解釋換門機率是由「第一次選門×換門」組成
然後由於本來中的換了必定不中,本來不中的換了必定中,所以「換門」部分的機率能視作1
也就是第一次選門便決定換門機率
其實我不太理解為什麼這樣會比較容易懂
會認為是1/2的思路是「認為只剩2扇門,2選1就是1/2」
這種說明方式結果還是剩2扇門啊
應該要解釋換門機率是由「第一次選門×換門」組成
然後由於本來中的換了必定不中,本來不中的換了必定中,所以「換門」部分的機率能視作1
也就是第一次選門便決定換門機率
無題 無名 21/01/11(一)21:49:41 ID:UaoXYUWk No.2185291
我是不是走錯版 這邊是歡樂惡搞?
摳男說得好 「真相只有一個」
怎麼換都是一樣 沒有機率比較高這回事
摳男說得好 「真相只有一個」
怎麼換都是一樣 沒有機率比較高這回事
>>2185291
>怎麼換都是一樣 沒有機率比較高這回事
確實是有比較高
因為主持人幫你刪去一個錯誤選項了
好 現在當大家數學不好 不要講數學
你完全撇去計算
一開始你在選門 兩個摃龜 一個中獎
所以比起中獎比較可能的是一開始就摃龜 有道理吧?
然後現在主持人幫你刪掉一個選項
你一開始摃龜機率就已經比較大了
那是不是你換另一個中的可能性更高
已經完全不扯數學了這樣還不能理解就沒辦法
>怎麼換都是一樣 沒有機率比較高這回事
確實是有比較高
因為主持人幫你刪去一個錯誤選項了
好 現在當大家數學不好 不要講數學
你完全撇去計算
一開始你在選門 兩個摃龜 一個中獎
所以比起中獎比較可能的是一開始就摃龜 有道理吧?
然後現在主持人幫你刪掉一個選項
你一開始摃龜機率就已經比較大了
那是不是你換另一個中的可能性更高
已經完全不扯數學了這樣還不能理解就沒辦法
無題 無名 21/01/11(一)21:59:05 ID:hyuUhzSc No.2185296
我覺得機率會變
開門給你選1/2機率
這樣第一個選的門錯誤換門機率變高
開門給你選1/2機率
這樣第一個選的門錯誤換門機率變高
無題 無名 21/01/11(一)21:59:29 ID:PRHvf.As No.2185297
無題 無名 21/01/11(一)22:05:13 ID:nrxw.egg No.2185300
>>2185291
趨近無限多道門,只有一道是通往出口,在第一次選擇時,你只能隨便選擇一扇,因為你不知道哪道是正確的
請問一下,你第一次就選擇到正確出口的機率是多少
此時,一個天使表示可以幫你刪去大多數的門,只剩下另外一道可能是出口的門來考慮,但她也表示你可以堅持你第一道選的門
你覺得你要堅持我有主角光環、天選之人最初選的門就是出口,還是走向天使幫你篩出來的那道可能是出口的門
趨近無限多道門,只有一道是通往出口,在第一次選擇時,你只能隨便選擇一扇,因為你不知道哪道是正確的
請問一下,你第一次就選擇到正確出口的機率是多少
此時,一個天使表示可以幫你刪去大多數的門,只剩下另外一道可能是出口的門來考慮,但她也表示你可以堅持你第一道選的門
你覺得你要堅持我有主角光環、天選之人最初選的門就是出口,還是走向天使幫你篩出來的那道可能是出口的門
無題 無名 21/01/11(一)22:05:30 ID:Pa.ZRaQw No.2185301
>>2185284
>會認為是1/2的思路是「認為只剩2扇門,2選1就是1/2」
>這種說明方式結果還是剩2扇門啊
因為我身邊很多聽不懂的人都是在1/3選門跟主持人刪除剩1/2這邊無法理解差異就停止思考 所以他們無法理解換門為什麼有機率上的意義才會跳到「認為只剩2扇門,2選1就是1/2」
今天換成10扇門 甚至100扇門 他們才會意識到
(1)第一次就選到大獎門的機率是比較低的
(2)主持人刪除了98個錯誤選項的這個動作對於機率的影響
要先最簡單的讓他們認知到上面這兩個動作意義為何,他們才會往下理解 不然就是死機直接跳到最終的「二選一=50%」
>會認為是1/2的思路是「認為只剩2扇門,2選1就是1/2」
>這種說明方式結果還是剩2扇門啊
因為我身邊很多聽不懂的人都是在1/3選門跟主持人刪除剩1/2這邊無法理解差異就停止思考 所以他們無法理解換門為什麼有機率上的意義才會跳到「認為只剩2扇門,2選1就是1/2」
今天換成10扇門 甚至100扇門 他們才會意識到
(1)第一次就選到大獎門的機率是比較低的
(2)主持人刪除了98個錯誤選項的這個動作對於機率的影響
要先最簡單的讓他們認知到上面這兩個動作意義為何,他們才會往下理解 不然就是死機直接跳到最終的「二選一=50%」
無題 無名 21/01/11(一)22:13:46 ID:EZzaN/BY No.2185304
>>2185302
題目怪怪的...
三囚問題不是死兩個嗎?
題目怪怪的...
三囚問題不是死兩個嗎?
>>2185302
" 詔獄中有甲、乙、丙三個死囚,新任皇帝加冕之日,決定在次日特赦其中一位囚犯作為慶祝,但要將另兩位處決。皇帝抽籤選出那位幸運的囚犯之後,告訴典獄長,哪兩位囚犯將要被處死,哪一位囚犯將要被赦免。但皇帝特別要求典獄長,不可讓死囚知曉自己即將被處死或被特赦。
甲聽聞了皇帝即將赦免三人中的一人,趕緊私下向典獄長詢問自己未來的情況,典獄長答:「奉上諭,我不能讓你知道,你會被赦免或者處決。所以我只告訴你,乙會遭處決。」甲聽說乙會被處決後,非常高興,認為現在只有自己跟丙可能會被赦免,所以自己有五成的機會被赦免,甲高興地一五一十地告訴了副典獄長,副典獄長卻說:「不對,你只有三分之一的機會被赦免。」究竟何者為真呢?"
三囚類似但是不完全跟三門一樣,它更直觀的去挑戰了人類常識的盲點
三名死囚只有一位會被赦免,每個人存活的機率是1/3
而知道其中一人已經被處死後剩下兩人一定有一人會死一人會活
一般常識思考就會卡住認為剩下的機率是50/50
但是打一開始赦免一人處死兩人的規則從來沒有變過,三民死囚無論如何存活的機率都會是1/3
" 詔獄中有甲、乙、丙三個死囚,新任皇帝加冕之日,決定在次日特赦其中一位囚犯作為慶祝,但要將另兩位處決。皇帝抽籤選出那位幸運的囚犯之後,告訴典獄長,哪兩位囚犯將要被處死,哪一位囚犯將要被赦免。但皇帝特別要求典獄長,不可讓死囚知曉自己即將被處死或被特赦。
甲聽聞了皇帝即將赦免三人中的一人,趕緊私下向典獄長詢問自己未來的情況,典獄長答:「奉上諭,我不能讓你知道,你會被赦免或者處決。所以我只告訴你,乙會遭處決。」甲聽說乙會被處決後,非常高興,認為現在只有自己跟丙可能會被赦免,所以自己有五成的機會被赦免,甲高興地一五一十地告訴了副典獄長,副典獄長卻說:「不對,你只有三分之一的機會被赦免。」究竟何者為真呢?"
三囚類似但是不完全跟三門一樣,它更直觀的去挑戰了人類常識的盲點
三名死囚只有一位會被赦免,每個人存活的機率是1/3
而知道其中一人已經被處死後剩下兩人一定有一人會死一人會活
一般常識思考就會卡住認為剩下的機率是50/50
但是打一開始赦免一人處死兩人的規則從來沒有變過,三民死囚無論如何存活的機率都會是1/3
無題 無名 21/01/11(一)22:21:10 ID:wyjYMHW. No.2185306
>>2185281
這就是愚昧之人為自己開脫的方法嗎?
這就是愚昧之人為自己開脫的方法嗎?
無題 無名 21/01/11(一)22:22:17 ID:h53FuKuY No.2185307
>>2185291
看像你這樣的笨蛋發言就是歡樂惡搞了
看像你這樣的笨蛋發言就是歡樂惡搞了
有種似曾相似的感覺
為什麼這個鴿子這麼大?
為什麼這個鴿子這麼大?
無題 無名 21/01/11(一)22:29:40 ID:ivMAnPbw No.2185312
>>2185291
感謝你把這邊變回歡樂惡搞
感謝你把這邊變回歡樂惡搞
無題 無名 21/01/11(一)22:31:39 ID:3UbO7NbM No.2185313
無題 無名 21/01/11(一)22:43:00 ID:nrxw.egg No.2185318
肛交惡徒想要尋找新的肛交器,很不幸地你被看上了,其中有14億-1的韭菜和1個可以帶你逃走的真正朋友,你可以隨便在茫茫人海中找一個人,然後選擇信賴他會帶你逃走
此刻,你接到一個線報,告訴你有另外一個潛在的人可能是真的朋友,但不確定你現在找的這個人是不是韭菜,這時你面臨一個問題
是要拋棄你萍水相逢找到的這個夥伴,還是堅持相信你自己的直覺?
此刻,你接到一個線報,告訴你有另外一個潛在的人可能是真的朋友,但不確定你現在找的這個人是不是韭菜,這時你面臨一個問題
是要拋棄你萍水相逢找到的這個夥伴,還是堅持相信你自己的直覺?
>>2185310
我看後續的問題是
ABC 三個犯人 會赦免 1個 另外兩個死刑
而獄卒本人知道有誰會被赦免
A問了獄卒 B.C誰會被判死刑
如果今天赦免的是 B
獄卒會回答 C 被判死刑
如果今天赦免的是 C
獄卒會回答 B 被判死刑
如果今天赦免的是 A
獄卒會丟銅板決定要回答 B 或 C
獄卒回答了 A
B 被判死刑了
A 告訴 C
太好了 只剩你跟我 所以我赦免的機率變成1/2了
C 回答 A
不對 你赦免的機率只有1/3 不過我赦免的機率變成2/3了
----------------------------
我看後續的問題是
ABC 三個犯人 會赦免 1個 另外兩個死刑
而獄卒本人知道有誰會被赦免
A問了獄卒 B.C誰會被判死刑
如果今天赦免的是 B
獄卒會回答 C 被判死刑
如果今天赦免的是 C
獄卒會回答 B 被判死刑
如果今天赦免的是 A
獄卒會丟銅板決定要回答 B 或 C
獄卒回答了 A
B 被判死刑了
A 告訴 C
太好了 只剩你跟我 所以我赦免的機率變成1/2了
C 回答 A
不對 你赦免的機率只有1/3 不過我赦免的機率變成2/3了
----------------------------
無題 無名 21/01/11(一)22:54:31 ID:5yBbCKkw No.2185322
騙人的影片
車在B怎麼換也不會跑去AC
換不換又沒差
車在B怎麼換也不會跑去AC
換不換又沒差
>>2185323
你都說無法選擇了為什麼發問會改機率......
你都說無法選擇了為什麼發問會改機率......
無題 無名 21/01/11(一)23:07:48 ID:Y8HPlujM No.2185325
通常大獎在C的機率高 主持人根本在騙 我一定選C
無題 無名 21/01/11(一)23:20:59 ID:nrxw.egg No.2185328
某個不知名的小國家,在大選後被告知,三組候選人中有兩組舔共
投了A黨的甲焦急萬分,怕自己投給了舔共黨
這時,B黨爆出醜聞,確定他們的候選人舔共
投了A黨的甲這時興奮的大叫:不怕!相信黨!
投給C黨的乙則不以為然,認為甲的黨才舔共
請問甲投了舔共黨的機率是多少?乙投給舔共黨的機率又是多少?
投了A黨的甲焦急萬分,怕自己投給了舔共黨
這時,B黨爆出醜聞,確定他們的候選人舔共
投了A黨的甲這時興奮的大叫:不怕!相信黨!
投給C黨的乙則不以為然,認為甲的黨才舔共
請問甲投了舔共黨的機率是多少?乙投給舔共黨的機率又是多少?
無題 無名 21/01/12(二)00:06:24 ID:Mslc4atE No.2185337
>>2185324
因為事件會因為問的人是誰而改變
因為事件會因為問的人是誰而改變
無題 無名 21/01/12(二)00:09:14 ID:aw8ZC/T2 No.2185338
>>2185295
所以你現在懂我為什麼要換成十門說明了吧
有些人就是不懂數學 只用他們平常的邏輯來思考
你用數學或計算的方式解釋他就是不能理解 為甚麼換門機率會比較高
不先讓他們理解到
(1)第一次就選到大獎門的機率是比較低的
(2)主持人刪除了XX個錯誤選項的這個動作對於機率的影響
就往下談他們只會死機然後跳到他們容易理解的地方 溝通就不會繼續
所以你現在懂我為什麼要換成十門說明了吧
有些人就是不懂數學 只用他們平常的邏輯來思考
你用數學或計算的方式解釋他就是不能理解 為甚麼換門機率會比較高
不先讓他們理解到
(1)第一次就選到大獎門的機率是比較低的
(2)主持人刪除了XX個錯誤選項的這個動作對於機率的影響
就往下談他們只會死機然後跳到他們容易理解的地方 溝通就不會繼續
或許我是笨蛋 但是換個思考想
雖然有三道門 兩羊一車 但是只有兩種結果 中車中羊
不管怎麼選 其中一隻羊的門一定會被主持人剃除
所以我們的選則 就是中車 跟 中羊 的兩個結果而已
卻被這莫名其妙的心理數學 什麼三分之一 重選機率還會變 耍得團團轉
車子在現實上就是停在那扇門後面 不會因為你重新選則就跑來跑去變換位子
運氣沒有機率 有的只有必然
雖然有三道門 兩羊一車 但是只有兩種結果 中車中羊
不管怎麼選 其中一隻羊的門一定會被主持人剃除
所以我們的選則 就是中車 跟 中羊 的兩個結果而已
卻被這莫名其妙的心理數學 什麼三分之一 重選機率還會變 耍得團團轉
車子在現實上就是停在那扇門後面 不會因為你重新選則就跑來跑去變換位子
運氣沒有機率 有的只有必然
完全搞懂了
那麼問題來了
有什麼情況是能讓我應用到這個理論?
那麼問題來了
有什麼情況是能讓我應用到這個理論?
無題 無名 21/01/12(二)03:11:40 ID:wnOtvkps No.2185361
>>2185359
雖然知道你真的很笨
既然你都知道只有一扇門後面有車
3門中只有1門是車,所以一次開中車
當然就是三分之一的機會
如果認為只有中和不中、二分之一,只是沒理會過機率的存在
假如我增多門的數量
4門中只有1門是車,所以一次開中車就是四分之一的機會
5門中只有1門是車,所以一次開中車就是五分之一的機會
6門中只有1門是車,所以一次開中車就是六分之一的機會
……如此類推
100門中只有1門是車,所以一次開中車就是百分之一的機會
所以從來都不是二分之一
雖然知道你真的很笨
既然你都知道只有一扇門後面有車
3門中只有1門是車,所以一次開中車
當然就是三分之一的機會
如果認為只有中和不中、二分之一,只是沒理會過機率的存在
假如我增多門的數量
4門中只有1門是車,所以一次開中車就是四分之一的機會
5門中只有1門是車,所以一次開中車就是五分之一的機會
6門中只有1門是車,所以一次開中車就是六分之一的機會
……如此類推
100門中只有1門是車,所以一次開中車就是百分之一的機會
所以從來都不是二分之一
無題 無名 21/01/12(二)03:36:59 ID:H0yd83B6 No.2185362
>>2185360
聊天的時候發現有人怎麼講都不懂就可以跟他賭錢賺外快用
聊天的時候發現有人怎麼講都不懂就可以跟他賭錢賺外快用
無題 無名 21/01/12(二)03:46:50 ID:FRTPxWTM No.2185363
>>2185360
如果不知道學會了一個新知識有什麼用途,至少能讓你不會因為沒有那份知識而被騙
如果不知道學會了一個新知識有什麼用途,至少能讓你不會因為沒有那份知識而被騙
無題 無名 21/01/12(二)08:06:02 ID:zWVm5xMk No.2185379
>>2185365
不然怎麼博弈業會這麼興盛 包括抽卡手游
不然怎麼博弈業會這麼興盛 包括抽卡手游
無題 無名 21/01/12(二)10:24:00 ID:qmCc2mSw No.2185404
>>2185403
所以你200元發票有這樣多中幾張嗎?
所以你大樂透有中過嗎?
所以你老闆幫你加薪了嗎?
所以你有妹妹嗎? (除了妄想的以外)
所以你有老婆嗎? (除了手機遊戲跟右手外)
所以你爸是李剛/郭台銘嗎?
所以你是神豬嗎? (有500萬美金可以玩)
把你的雞雞收起來! 快去睡覺!
所以你200元發票有這樣多中幾張嗎?
所以你大樂透有中過嗎?
所以你老闆幫你加薪了嗎?
所以你有妹妹嗎? (除了妄想的以外)
所以你有老婆嗎? (除了手機遊戲跟右手外)
所以你爸是李剛/郭台銘嗎?
所以你是神豬嗎? (有500萬美金可以玩)
把你的雞雞收起來! 快去睡覺!
無題 無名 21/01/12(二)10:27:08 ID:QPp1OtyA No.2185407
無題 無名 21/01/12(二)11:07:08 ID:qmCc2mSw No.2185419
>>2185360
>>2185405
常見的機率應用範圍
五花八門的生活中充滿許許多多的變異,人們又該如何去發現其行蹤
而加以處理。下列舉出一些平時常見的生活機率例子供做參考。
1.醫學:疾病之發生率、誤診之可能性、藥物之治療率。
2.工業:產品之瑕疵及可靠性(或故障率)、勞動率。
3.商業:經濟成長率、投資的風險性、通貨膨脹率、進出口比率、競爭力。
4.人文社會:失業率、犯罪率、死亡率、人口成長率、保險率、離婚率。
5.其他:勝算率、得分率、命中率、中獎的可能性、銷售率。
是的
以上是我隨便就在網上搜到的機率應用範疇
自己無知沒有錯,不知道一個新知識有什麼用途,可以自己找找
但無知還這麼大聲,好像理直氣壯卻又不求甚解的笨蛋
我們一般會形容這種人為白目
>>2185405
常見的機率應用範圍
五花八門的生活中充滿許許多多的變異,人們又該如何去發現其行蹤
而加以處理。下列舉出一些平時常見的生活機率例子供做參考。
1.醫學:疾病之發生率、誤診之可能性、藥物之治療率。
2.工業:產品之瑕疵及可靠性(或故障率)、勞動率。
3.商業:經濟成長率、投資的風險性、通貨膨脹率、進出口比率、競爭力。
4.人文社會:失業率、犯罪率、死亡率、人口成長率、保險率、離婚率。
5.其他:勝算率、得分率、命中率、中獎的可能性、銷售率。
是的
以上是我隨便就在網上搜到的機率應用範疇
自己無知沒有錯,不知道一個新知識有什麼用途,可以自己找找
但無知還這麼大聲,好像理直氣壯卻又不求甚解的笨蛋
我們一般會形容這種人為白目
無題 無名 21/01/12(二)13:04:19 ID:nH6BcqZ6 No.2185444
問最後剩下兩道門選擇 中獎的機率未何 a門 跟b門
現在“聰明人們”的主張如下
若一開使就選a 在剩下兩道門中二分之一的選擇中 不換選擇 繼續選a 中獎是三分之一
若是一開始選a 在剩下兩道門中二分之一的選擇換門 選擇b 則是中獎三分之二
然後解釋方式是 三分之一 等於100分之一
因為”聰明人們“ 要別人跟他們一樣這樣糾結在前面三選一之中 因為比他們聰明的人也是這樣說的
一開始確實是三分一 但是 去掉一扇門後的選擇 卻還是要保持之前的三分之一機率 重新選擇的時候機率就因該更變了 但是“聰明人們”不準你們這樣想
所以三扇門中有一個門中獎 去掉一個門之後 jackie 的鼻子有幾個
現在“聰明人們”的主張如下
若一開使就選a 在剩下兩道門中二分之一的選擇中 不換選擇 繼續選a 中獎是三分之一
若是一開始選a 在剩下兩道門中二分之一的選擇換門 選擇b 則是中獎三分之二
然後解釋方式是 三分之一 等於100分之一
因為”聰明人們“ 要別人跟他們一樣這樣糾結在前面三選一之中 因為比他們聰明的人也是這樣說的
一開始確實是三分一 但是 去掉一扇門後的選擇 卻還是要保持之前的三分之一機率 重新選擇的時候機率就因該更變了 但是“聰明人們”不準你們這樣想
所以三扇門中有一個門中獎 去掉一個門之後 jackie 的鼻子有幾個
>>2185437
等等..你知道你提出的東西裡面一堆都不是機率 而是整體百分比 跟前年數字比較後的差距比例的東西嗎 該不會只是把有“率”字都打上來吧 都懷疑你在反串了
等等..你知道你提出的東西裡面一堆都不是機率 而是整體百分比 跟前年數字比較後的差距比例的東西嗎 該不會只是把有“率”字都打上來吧 都懷疑你在反串了
無題 無名 21/01/12(二)13:22:10 ID:nH6BcqZ6 No.2185453
>>2185451
聰明人你好
聰明人你好
無題 無名 21/01/12(二)13:31:59 ID:NnyOdL4s No.2185455
無題 無名 21/01/12(二)13:36:51 ID:LXHbJEjc No.2185456
>>2184869
And I took that personally
And I took that personally
>>2185444
文院和管院最常出現的碩士考科就是統計
機率只是這個科目的基礎
因為這些科目要走深的基本工就是資料分析
如何看出未來趨勢和相關性 以及分析的信心水準
當然中間去掉脈絡就會變成海道造成全球暖化這種笑話
文院和管院最常出現的碩士考科就是統計
機率只是這個科目的基礎
因為這些科目要走深的基本工就是資料分析
如何看出未來趨勢和相關性 以及分析的信心水準
當然中間去掉脈絡就會變成海道造成全球暖化這種笑話
無題 無名 21/01/12(二)13:37:23 ID:NnyOdL4s No.2185458
>>2185457
更正社科院和管院
更正社科院和管院
>>2185444
說了半天,原來你還是沒搞懂的那個
放大到100原意只是要你看清楚,一開始會選中的百份比是有差的,放到100一般人應該就會理解到,一開始就會選中是有多少的機會
你卡著的地方就是以為換門等於重新選擇
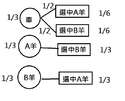
完全理解錯了
首先並不是重新選擇,因為先前是三選一,你不換,依然是三選一沒變過,所以機率根本沒有被重置
說了半天,原來你還是沒搞懂的那個
放大到100原意只是要你看清楚,一開始會選中的百份比是有差的,放到100一般人應該就會理解到,一開始就會選中是有多少的機會
你卡著的地方就是以為換門等於重新選擇
完全理解錯了
首先並不是重新選擇,因為先前是三選一,你不換,依然是三選一沒變過,所以機率根本沒有被重置
無題 無名 21/01/12(二)14:33:05 ID:qmCc2mSw No.2185477
無題 無名 21/01/12(二)14:53:14 ID:Y45Q1Yfs No.2185482
無題 無名 21/01/12(二)15:04:39 ID:MJ6fuCVc No.2185484
>>2185463
補充
你不要說得好像是什麼聰明人在誤導你,雖然聽你這麼說已經知道你真的不大聰明
但這只是一個數學問題,有學過數學的都能搞懂,不是什麼多聰明的問題,只是這問題看起來很違反直覺,簡易讓人跌入是1/2這陷阱
開始是1/3這既定事實,你是不可以忽略他來計算的
如果你只著眼只有中和不中,就是1/2,那你永遠也不可能搞懂這題目
補充
你不要說得好像是什麼聰明人在誤導你,雖然聽你這麼說已經知道你真的不大聰明
但這只是一個數學問題,有學過數學的都能搞懂,不是什麼多聰明的問題,只是這問題看起來很違反直覺,簡易讓人跌入是1/2這陷阱
開始是1/3這既定事實,你是不可以忽略他來計算的
如果你只著眼只有中和不中,就是1/2,那你永遠也不可能搞懂這題目
無題 無名 21/01/12(二)15:30:05 ID:lNtr8TVs No.2185492
你第一次的選擇是1/N機會命中,最後節目會排除(N-2)的門
所以最後的命中率會變成1/2,但提前你要再選擇一次,而且不能選本來的,否則你便沒有脫離1/N機會命中的命運
只要你冷靜想一想,你有可能1/N的機率一擊即中嗎?那你就會果斷不戴套了
所以最後的命中率會變成1/2,但提前你要再選擇一次,而且不能選本來的,否則你便沒有脫離1/N機會命中的命運
只要你冷靜想一想,你有可能1/N的機率一擊即中嗎?那你就會果斷不戴套了
無題 無名 21/01/12(二)15:32:44 ID:6z/N6dgk No.2185494
我是不知道到底是1/2還1/3拉
但我清楚反正那些嘴一堆的人根本沒機會去驗證
因為你根本沒機會上那種節目參加選擇遊戲
就算參加了也抽不到
所以機率等於零
不是什麼1/2 1/3 2/3
如果是台灣節目更不用講都是假的
你抽到也會要你退還w
但我清楚反正那些嘴一堆的人根本沒機會去驗證
因為你根本沒機會上那種節目參加選擇遊戲
就算參加了也抽不到
所以機率等於零
不是什麼1/2 1/3 2/3
如果是台灣節目更不用講都是假的
你抽到也會要你退還w
>>2185444
您不好的應該是國文閱讀能力才對,因為整場遊戲就是從「你去從N個門中選一個」開始
假設您完全不換門,那您抽中的機會只會是(1/門數)
您大可以當作「有人來去掉其他門」這件事沒有發生,因為自始至終,你做的選擇就是從那N個門中去選一個
假設你願意換門,「有人來去掉其他門」這件事有發生,「這個事件之後」的遊戲機率雖然有改變
但是這件事改變不了遊戲的「起點」就是「你去從N個門中選一個」開始
而你就堅持在「有人來改變條件了,所以遊戲的起點要重新算」這件事情上
但是就旁觀者而言,從你開始玩這個遊戲,起點就在「你去從N個門中選一個」開始,不管中間發生什麼事件,都不會改變
您不好的應該是國文閱讀能力才對,因為整場遊戲就是從「你去從N個門中選一個」開始
假設您完全不換門,那您抽中的機會只會是(1/門數)
您大可以當作「有人來去掉其他門」這件事沒有發生,因為自始至終,你做的選擇就是從那N個門中去選一個
假設你願意換門,「有人來去掉其他門」這件事有發生,「這個事件之後」的遊戲機率雖然有改變
但是這件事改變不了遊戲的「起點」就是「你去從N個門中選一個」開始
而你就堅持在「有人來改變條件了,所以遊戲的起點要重新算」這件事情上
但是就旁觀者而言,從你開始玩這個遊戲,起點就在「你去從N個門中選一個」開始,不管中間發生什麼事件,都不會改變
無題 無名 21/01/12(二)16:29:47 ID:HYIpXbHQ No.2185509
>>2185502
你是不是那種數學題目出現雞兔同籠問題時 拼命跟老師盧這兩種動物關在一起可能會打架所以不現實的人?
你是不是那種數學題目出現雞兔同籠問題時 拼命跟老師盧這兩種動物關在一起可能會打架所以不現實的人?
無題 無名 21/01/12(二)17:15:47 ID:qmCc2mSw No.2185519
>>2185502
你是不是那種打開數學課本就說『現實中根本不會有人買這麼多西瓜好嗎』的那種人…
你是不是那種打開數學課本就說『現實中根本不會有人買這麼多西瓜好嗎』的那種人…
無題 無名 21/01/12(二)17:23:36 ID:AcdIehKU No.2185520
>>2185505
應該這麼說
「換門後中車的機率」詳細說法是「選了一扇門,換門後中車的機率」
這個比較像文字陷阱
乍看之下以為只有換門之後「車子在門後機率」這件事
實際上你要「換門」就必須要先有「選門」這個行為
應該這麼說
「換門後中車的機率」詳細說法是「選了一扇門,換門後中車的機率」
這個比較像文字陷阱
乍看之下以為只有換門之後「車子在門後機率」這件事
實際上你要「換門」就必須要先有「選門」這個行為
無題 無名 21/01/12(二)17:34:36 ID:AcdIehKU No.2185523
>>2185522
網路上也有小學生科展的驗證資料w
網路上也有小學生科展的驗證資料w
無題 無名 21/01/12(二)17:38:24 ID:OYuaq75g No.2185525
機率由主持強制開了一扇門的這一動作當下就變了
就算我沒換也只是代表我由餘下兩扇門中選擇了最初那扇門
根本無關我有沒有選另一扇門才改變機率
就算我沒換也只是代表我由餘下兩扇門中選擇了最初那扇門
根本無關我有沒有選另一扇門才改變機率
馬的這個問題不就是高中課程的條件機率
不會的人回去翻一下課本好嗎?
不會的人回去翻一下課本好嗎?
無題 無名 21/01/12(二)17:46:19 ID:qmCc2mSw No.2185531
>>2185528
等等,你真的覺得上面沒懂的人有高中程度嗎?
等等,你真的覺得上面沒懂的人有高中程度嗎?
這串本身就來亂的吧
根本不是歡樂惡搞內容
不就綜合跟四格某些人嘴不贏才跑來這重新開串釣魚wwwwwwwwwww
機率永遠不變 好嗎 文組實在很悲哀
根本不是歡樂惡搞內容
不就綜合跟四格某些人嘴不贏才跑來這重新開串釣魚wwwwwwwwwww
機率永遠不變 好嗎 文組實在很悲哀
無題 無名 21/01/12(二)18:18:04 ID:AcdIehKU No.2185535
>>2185532
複雜點才能歡樂
門多點就能看出性質
假設有5門4羊1車,選擇一扇門後主持人開啟一扇有羊的門
那麼
一開始選中獎門,不換門的中獎機率是:
1/5(選中獎門)×1/2(不換門)×1(必中)=1/10
一開始選中獎門,換門的中獎機率是:
1/5×1/2(換門)×0(不可能)=0
一開始選中獎門,不換門的不中獎機率是:
1/5×1/2×0=0
一開始選中獎門,換門的不中獎機率是:
1/5×1/2×1=1/10
一開始選不中獎門,換門的中獎機率是:
4/5×1/2×1/3(剩3扇門只有1扇中獎)=2/15
一開始選不中獎門,不換門的中獎機率是:
4/5×1/2×0=0
一開始選不中獎門,換門的不中獎機率是:
4/5×1/2×2/3(剩3扇門有2扇不中獎)=4/15
一開始選不中獎門,不換門的不中獎機率是:
4/5×1/2×1=2/5
所以換門中獎機率是由
一開始選中獎門,換門的中獎機率
一開始選不中獎門,換門的中獎機率
組成
且因為只看換門(或不換門),可以省去換門與否的1/2
是故換門中獎機率=(1/5×0)+(4/5×1/3)=4/15
而不換門中獎機率=(1/5×1)+(4/5×0)=1/5
看起來有趣多了吧
複雜點才能歡樂
門多點就能看出性質
假設有5門4羊1車,選擇一扇門後主持人開啟一扇有羊的門
那麼
一開始選中獎門,不換門的中獎機率是:
1/5(選中獎門)×1/2(不換門)×1(必中)=1/10
一開始選中獎門,換門的中獎機率是:
1/5×1/2(換門)×0(不可能)=0
一開始選中獎門,不換門的不中獎機率是:
1/5×1/2×0=0
一開始選中獎門,換門的不中獎機率是:
1/5×1/2×1=1/10
一開始選不中獎門,換門的中獎機率是:
4/5×1/2×1/3(剩3扇門只有1扇中獎)=2/15
一開始選不中獎門,不換門的中獎機率是:
4/5×1/2×0=0
一開始選不中獎門,換門的不中獎機率是:
4/5×1/2×2/3(剩3扇門有2扇不中獎)=4/15
一開始選不中獎門,不換門的不中獎機率是:
4/5×1/2×1=2/5
所以換門中獎機率是由
一開始選中獎門,換門的中獎機率
一開始選不中獎門,換門的中獎機率
組成
且因為只看換門(或不換門),可以省去換門與否的1/2
是故換門中獎機率=(1/5×0)+(4/5×1/3)=4/15
而不換門中獎機率=(1/5×1)+(4/5×0)=1/5
看起來有趣多了吧
一名在太空中旅行的人很久沒有找到適合居住的類地行星了,而他在浩瀚的宇宙中無意間發現了一個類地星球,但不確定能不能住,總之就先降落看看
這時,透過電波擷取,一名太空嚮導說他有發現另一個可能才是適合他居住的星球,但旅人的那顆星球也可能是旅人真正想找的那一個
如果你是太空旅人,你會堅持自己發現的那顆星球才是真正你要找的星球,還是前往嚮導所說的那顆星球?
這時,透過電波擷取,一名太空嚮導說他有發現另一個可能才是適合他居住的星球,但旅人的那顆星球也可能是旅人真正想找的那一個
如果你是太空旅人,你會堅持自己發現的那顆星球才是真正你要找的星球,還是前往嚮導所說的那顆星球?
這串只讓我想到以前那個三人買東西
花了多少剩下多少騙人的題目
就各種方式去騙邏輯能力差的人
也改變不了機率多寡的問題
換了機率提升? 整個就很可笑
花了多少剩下多少騙人的題目
就各種方式去騙邏輯能力差的人
也改變不了機率多寡的問題
換了機率提升? 整個就很可笑
繼續吐槽
管你是1/3 1/10 1/100 或 1/10000
你一開始選擇權只有一次 那就是正常機率
給你機會換 只要分母沒變 機率就不會改變
只是重新選擇一次相同機率罷了
文組數學就很喜歡搞文字遊戲來騙人
從這次的1/100換去另一個也一樣是1/100 門又沒開過半個 機率最好是會變拉(攤
管你是1/3 1/10 1/100 或 1/10000
你一開始選擇權只有一次 那就是正常機率
給你機會換 只要分母沒變 機率就不會改變
只是重新選擇一次相同機率罷了
文組數學就很喜歡搞文字遊戲來騙人
從這次的1/100換去另一個也一樣是1/100 門又沒開過半個 機率最好是會變拉(攤
無題 無名 21/01/12(二)19:20:38 ID:HokMX9uY No.2185544
所有認為機率不變的人,我拿出110萬,你拿出90萬
你做開門的哪位,每次賭金10萬,我選中了我得10萬,選錯了你得10萬
你有得賺喔
你做開門的哪位,每次賭金10萬,我選中了我得10萬,選錯了你得10萬
你有得賺喔
無題 無名 21/01/12(二)19:21:57 ID:0jD3Bblw No.2185545
無題 無名 21/01/12(二)20:02:16 ID:HhwUMM7A No.2185552
挺機率比較高的人是不是認為
你玩手遊網遊課金後
點下要抽一次獎跳出選項問你[確定] [取消]時候
只要多選幾次取消就有機會當歐洲人 是嗎wwwwwwwwwwwwww
難怪遊戲公司那麼好賺w
你玩手遊網遊課金後
點下要抽一次獎跳出選項問你[確定] [取消]時候
只要多選幾次取消就有機會當歐洲人 是嗎wwwwwwwwwwwwww
難怪遊戲公司那麼好賺w
無題 無名 21/01/12(二)21:07:30 ID:esJvM4Z2 No.2185567
無題 無名 21/01/12(二)21:08:53 ID:MvfnPmjU No.2185568
>>2185542
自己文盲讀不懂題目怪別人文組數學w
你知道你自己的發言已經支離滅裂了嗎?
> 給你機會換 只要分母沒變 機率就不會改變
你知道強制開門這個動作就是改變分母了嗎?
>只是重新選擇一次相同機率罷了
你抽完一支籤,台主把其它不會中的籤都強制抽掉,只留下一支,問你換不換
結果你回答分母沒變,機率是相等的,所以你只相信自己www
自己文盲讀不懂題目怪別人文組數學w
你知道你自己的發言已經支離滅裂了嗎?
> 給你機會換 只要分母沒變 機率就不會改變
你知道強制開門這個動作就是改變分母了嗎?
>只是重新選擇一次相同機率罷了
你抽完一支籤,台主把其它不會中的籤都強制抽掉,只留下一支,問你換不換
結果你回答分母沒變,機率是相等的,所以你只相信自己www
到底真的有這麼多智障還是在釣魚
無題 無名 21/01/12(二)21:30:24 ID:WrVDlXNc No.2185572
>>2185560
這什麼莫名其妙的類比...
手遊的卡池機制跟蒙提霍爾問題是一樣的嗎?
照你這樣硬扯也不是不行啦 但是抽卡機制就會完全不一樣了
遊戲今天從卡池中隨機抽出五張未掀開的角色卡
系統提示你是一張SSR電子老婆+4張大甲芋頭(芋ABCD)
(這款遊戲完全公平不存在機率操作等手段 避免又有人節外生枝)
五張選一張 即是1/5抽種電子老婆4/5中大甲芋頭
你可以先選定一張(非掀開) 遊戲會掀開三張大甲芋頭
這時場上未知的卡只有你選定的一張及系統保留的一張
此時有一次更換選定卡片的機會 你可以堅持不換或換卡
因為是兩張卡選一張所以就算堅持機率仍是1/2嗎?
錯了 因為你選定那張卡是在五張未知卡片時
所以機率還是1/5 列表如下
堅持不換
你選中老婆>不換>老婆get!!
你選中芋A>不換>芋A get!!
你選中芋B>不換>芋B get!!
你選中芋C>不換>芋C get!!
你選中芋D>不換>芋D get!!
你只有1/5的機會抽中老婆
而更換的結果呢
你選中老婆>更換>芋A/B/C/D get!!
你選中芋A>更換>老婆 get!!
你選中芋B>更換>老婆 get!!
你選中芋C>更換>老婆 get!!
你選中芋D>更換>老婆 get!!
你有4/5的機會把老婆抱回家
這什麼莫名其妙的類比...
手遊的卡池機制跟蒙提霍爾問題是一樣的嗎?
照你這樣硬扯也不是不行啦 但是抽卡機制就會完全不一樣了
遊戲今天從卡池中隨機抽出五張未掀開的角色卡
系統提示你是一張SSR電子老婆+4張大甲芋頭(芋ABCD)
(這款遊戲完全公平不存在機率操作等手段 避免又有人節外生枝)
五張選一張 即是1/5抽種電子老婆4/5中大甲芋頭
你可以先選定一張(非掀開) 遊戲會掀開三張大甲芋頭
這時場上未知的卡只有你選定的一張及系統保留的一張
此時有一次更換選定卡片的機會 你可以堅持不換或換卡
因為是兩張卡選一張所以就算堅持機率仍是1/2嗎?
錯了 因為你選定那張卡是在五張未知卡片時
所以機率還是1/5 列表如下
堅持不換
你選中老婆>不換>老婆get!!
你選中芋A>不換>芋A get!!
你選中芋B>不換>芋B get!!
你選中芋C>不換>芋C get!!
你選中芋D>不換>芋D get!!
你只有1/5的機會抽中老婆
而更換的結果呢
你選中老婆>更換>芋A/B/C/D get!!
你選中芋A>更換>老婆 get!!
你選中芋B>更換>老婆 get!!
你選中芋C>更換>老婆 get!!
你選中芋D>更換>老婆 get!!
你有4/5的機會把老婆抱回家
用一個倒轉的概念去理解吧
ABC共3對門
你打開了門A,而一開始只有1/3 機會選到車,所以門A是車的機會是1/3
現在門B被打開了,只剩下門C了
你選的門A是1/3機會得到車子,你想想喔
你現在的選擇只有1/3機會喔!!
那剩下的2/3在哪??
我們用上帝視野去解釋的話,假設門C就是車子
你選了門C再重選門A/B而得不到車子是1號情況
你選了門B再選門C而得到車子是2號情況
你選了門A再選門C而得到車子是3號情況
你選了門C而不再再重選得到車子是4號情況
你選了門B而不再再重選而得不到車子是5號情況
你選了門A而不再再重選而得不到車子是6號情況
好了,你不可能再有其他情況了吧?
你看看,你重選而得到車子的機會有多少?
2/3喔!!!
ABC共3對門
你打開了門A,而一開始只有1/3 機會選到車,所以門A是車的機會是1/3
現在門B被打開了,只剩下門C了
你選的門A是1/3機會得到車子,你想想喔
你現在的選擇只有1/3機會喔!!
那剩下的2/3在哪??
我們用上帝視野去解釋的話,假設門C就是車子
你選了門C再重選門A/B而得不到車子是1號情況
你選了門B再選門C而得到車子是2號情況
你選了門A再選門C而得到車子是3號情況
你選了門C而不再再重選得到車子是4號情況
你選了門B而不再再重選而得不到車子是5號情況
你選了門A而不再再重選而得不到車子是6號情況
好了,你不可能再有其他情況了吧?
你看看,你重選而得到車子的機會有多少?
2/3喔!!!
無題 無名 21/01/12(二)21:53:21 ID:jOFbHXb2 No.2185577
>>2185574
載老婆一起去大甲買啊
載老婆一起去大甲買啊
>>2185575
別試了,這麼簡單的經典數學題目都可以掙扎
我在上面>>No.2185197的維基附圖應該已經很直觀的解釋為什麼機率會是2/3而不是1/2了.這樣都不能理解那真的是智商問題
無論用多少方式去解釋,沒有邏輯觀念的劣等基因是不可能突破自己的極限的
別試了,這麼簡單的經典數學題目都可以掙扎
我在上面>>No.2185197的維基附圖應該已經很直觀的解釋為什麼機率會是2/3而不是1/2了.這樣都不能理解那真的是智商問題
無論用多少方式去解釋,沒有邏輯觀念的劣等基因是不可能突破自己的極限的
今天才看到這篇
覺得問題出在最後會是個二選一的情況
所以失敗率反而跟成功率掉換過來
會覺得換的機率比較高是來自舊母體中較高的失敗率
刪去錯誤選項這件事會形成一個新母體
等值提升其他未知選項的成功率(包含原本選的那個
故換跟不換都是等值
覺得問題出在最後會是個二選一的情況
所以失敗率反而跟成功率掉換過來
會覺得換的機率比較高是來自舊母體中較高的失敗率
刪去錯誤選項這件事會形成一個新母體
等值提升其他未知選項的成功率(包含原本選的那個
故換跟不換都是等值
無題 無名 21/01/12(二)22:39:53 ID:BKB1HMz. No.2185590
不相信的人自己找家人朋友實際實驗一下
只要測試次數夠多
換與不換中獎比例會接近2:1
只要測試次數夠多
換與不換中獎比例會接近2:1
無題 無名 21/01/12(二)22:45:26 ID:Y45Q1Yfs No.2185592
無題 無名 21/01/12(二)22:46:51 ID:HhwUMM7A No.2185593
>>2185587
整串看下來還可以理解錯誤
整串看下來還可以理解錯誤
無題 無名 21/01/12(二)23:07:41 ID:TQmrKBPs No.2185602
無題 無名 21/01/12(二)23:27:17 ID:Q.mUCOLk No.2185605
倒過來看不就好了
我選到中獎門然後換成其他門的機率是1/3
反而選到其他門換成中獎門是2/3
我選到中獎門然後換成其他門的機率是1/3
反而選到其他門換成中獎門是2/3
看看這樣解釋如何
1. 一開始隨機選一扇門,車在這扇門後面的機率是1/3,
在"其他兩扇門"後面的機率是2/3
2. 現在主持人從"其他兩扇門"之中開了一扇門,
但車在"其他兩扇門"後面的機率還是2/3,不會變
3. 不過現在"其他兩扇門"裡面有一扇你已經看到了不是了,
所以2/3的機率全部都算在"其他兩扇門"之中沒開的那扇門
所以嚴格來說沒有任何機率改變過
一開始的門還是1/3
"其他兩扇門"的總和還是2/3
只是現在"其他兩扇門"只剩下一扇沒開
1. 一開始隨機選一扇門,車在這扇門後面的機率是1/3,
在"其他兩扇門"後面的機率是2/3
2. 現在主持人從"其他兩扇門"之中開了一扇門,
但車在"其他兩扇門"後面的機率還是2/3,不會變
3. 不過現在"其他兩扇門"裡面有一扇你已經看到了不是了,
所以2/3的機率全部都算在"其他兩扇門"之中沒開的那扇門
所以嚴格來說沒有任何機率改變過
一開始的門還是1/3
"其他兩扇門"的總和還是2/3
只是現在"其他兩扇門"只剩下一扇沒開
>>2185606
不是這樣的
我上面有提到從其他觀點切入
假設某個人從後半開始看,只看到1扇開啟的門有羊,以及另外兩扇關著的門,對他來說兩扇門後是車的機率各是1/2
如此就能確定這兩扇門「門後是車」的機率確實會從1/3變成1/2
但是今天題目是「換門之後得到車」的機率
既然有換門,那自然要先有選門這一行為
然後再仔細分析「換門」這件事
選擇中的門,換門後必然不中
即是1/3×0=0
選擇不中的門,因為另一隻羊被主持人挑出來,所以換門必定中
即是2/3×1=2/3
最後把兩個可能加起來便是「選擇一扇門,換門後中車的機率」
0+2/3=2/3
不是這樣的
我上面有提到從其他觀點切入
假設某個人從後半開始看,只看到1扇開啟的門有羊,以及另外兩扇關著的門,對他來說兩扇門後是車的機率各是1/2
如此就能確定這兩扇門「門後是車」的機率確實會從1/3變成1/2
但是今天題目是「換門之後得到車」的機率
既然有換門,那自然要先有選門這一行為
然後再仔細分析「換門」這件事
選擇中的門,換門後必然不中
即是1/3×0=0
選擇不中的門,因為另一隻羊被主持人挑出來,所以換門必定中
即是2/3×1=2/3
最後把兩個可能加起來便是「選擇一扇門,換門後中車的機率」
0+2/3=2/3
無題 無名 21/01/13(三)00:05:05 ID:.Hf9Zb/A No.2185611
>>2185608
我們講的不衝突吧
除非是我有什麼定義問題
其實不需要假設某個人從後半開始看
只要說剩下兩扇門的時候丟硬幣重選也可以
我想這個問題最大的癥結其實是"換"跟"選"這兩個看似一樣卻完全不同的動作
"換"代表的是從"一個特定選項"改成"非該選項"
"選"則是從所有選項中"隨機"選擇一個
認為答案是1/2的人通常是認為"換"跟"選"都是兩扇門"選"一扇,所以不換也一樣
卻沒有注意到,不換並不是"隨機選"
我們講的不衝突吧
除非是我有什麼定義問題
其實不需要假設某個人從後半開始看
只要說剩下兩扇門的時候丟硬幣重選也可以
我想這個問題最大的癥結其實是"換"跟"選"這兩個看似一樣卻完全不同的動作
"換"代表的是從"一個特定選項"改成"非該選項"
"選"則是從所有選項中"隨機"選擇一個
認為答案是1/2的人通常是認為"換"跟"選"都是兩扇門"選"一扇,所以不換也一樣
卻沒有注意到,不換並不是"隨機選"
無題 無名 21/01/13(三)00:24:11 ID:1XVVb4YA No.2185614
無題 無名 21/01/13(三)00:26:41 ID:mMyz/S2g No.2185615
我覺得最大問題是
門後面到底有沒有車子可以抽
門後面到底有沒有車子可以抽
什麼換不換定律誰鳥他阿
狀況改變一下
要是三個門後面分別是
[史上最貴的名牌車+永久保固]
[一團黑影附加許多眼睛跟黑色的手]
[一群人圍著你鼓掌拍手並說おめでとう]
現在就問你敢不敢親自去選其中一扇門打開
狀況改變一下
要是三個門後面分別是
[史上最貴的名牌車+永久保固]
[一團黑影附加許多眼睛跟黑色的手]
[一群人圍著你鼓掌拍手並說おめでとう]
現在就問你敢不敢親自去選其中一扇門打開
小弟不才,雖然上面幾位數學高手解釋的道理都懂
但覺得困惑的地方是,如果假定問題中的參賽者有兩個,並各自選了兩扇不同的門
那麼雙方互換門後的抽到大獎的機率不是兩方都提高?
以下是我腦中模擬的情境
假設過年時A和B和一群人集資買了一本刮刮樂
一整本刮刮樂中必定有一張會是最大獎,A隨便選了一張,B也選了一張
旁邊的人一直刮出小獎,最後直到剩下A、B手上兩張刮刮樂時,最大獎都還是沒有開出
這時A跟B都想起了三門問題,於是他們互換了對方原本選擇的刮刮樂
但他們同時又發覺對方一開始選到小獎的機率也是跟自己一樣的
假設如果排除剛剛其他張抽到小獎的情況,現在的情況就是"一本刮刮樂只有兩張,只有一張有最大獎"
那麼他們到底是該換掉呢?還是不要換掉呢?
即使雙方交換了,等於雙方抽到大獎的機率都提高,換言雙方的抽到的機率也下降了
那是否意味著交換與不交換都不影響抽到大獎的結果?
但覺得困惑的地方是,如果假定問題中的參賽者有兩個,並各自選了兩扇不同的門
那麼雙方互換門後的抽到大獎的機率不是兩方都提高?
以下是我腦中模擬的情境
假設過年時A和B和一群人集資買了一本刮刮樂
一整本刮刮樂中必定有一張會是最大獎,A隨便選了一張,B也選了一張
旁邊的人一直刮出小獎,最後直到剩下A、B手上兩張刮刮樂時,最大獎都還是沒有開出
這時A跟B都想起了三門問題,於是他們互換了對方原本選擇的刮刮樂
但他們同時又發覺對方一開始選到小獎的機率也是跟自己一樣的
假設如果排除剛剛其他張抽到小獎的情況,現在的情況就是"一本刮刮樂只有兩張,只有一張有最大獎"
那麼他們到底是該換掉呢?還是不要換掉呢?
即使雙方交換了,等於雙方抽到大獎的機率都提高,換言雙方的抽到的機率也下降了
那是否意味著交換與不交換都不影響抽到大獎的結果?
>>2185623
什麼語言不選
偏偏選排版一跑掉就完蛋的python
雖然這也是k島的問題就是了...
什麼語言不選
偏偏選排版一跑掉就完蛋的python
雖然這也是k島的問題就是了...
無題 無名 21/01/13(三)01:21:55 ID:XT1khJI. No.2185628
>>2185624
我錯了...
我錯了...
>>2185622
要考慮條件機率啊
首先要AB都沒抽到,剩下的人才有辦法把其他獎刮完沒中
也就是說,其實你的題目前提就是大獎在AB之中
所以當然二選一,中獎機率就是各50%
或者說,因為只有2%的機率大獎在AB之中
所以A或B中獎的機率是2%×50%,還是1%喔
要考慮條件機率啊
首先要AB都沒抽到,剩下的人才有辦法把其他獎刮完沒中
也就是說,其實你的題目前提就是大獎在AB之中
所以當然二選一,中獎機率就是各50%
或者說,因為只有2%的機率大獎在AB之中
所以A或B中獎的機率是2%×50%,還是1%喔
無題 無名 21/01/13(三)01:44:26 ID:2ysZaHaA No.2185631
>>2185630
這好像也不是條件機率,算了能懂就好
這好像也不是條件機率,算了能懂就好
我覺得重不重選機率都是二分之一啊
這不是邏輯問題,而是文字遊戲了
這不是邏輯問題,而是文字遊戲了
>>2185633
如果你是在講開串的問題的話
不是文字遊戲 是個很經典的機率問題
我們換一個比喻來想像一下(數學上是一樣的)
情境是100選1
摸彩箱中有100顆球(材質、體積、重量、形狀等等都一樣,沒有做任何記號,除了用看的之外無法分辨不同)
裡面有1顆中獎球跟99顆未中獎
將這100顆球倒進一個無法觀測內部的箱子中
然後你現在把手伸進去用一個無法觀測內部的小盒子隨手裝了一顆球並把盒子鎖起來
接著把裝了一顆球的盒子拿出來之後放在旁邊
接下來 主持人在你取出一顆球的大箱子上面開了一個只有他能看到裡面的小開口
並把裡面的未中獎球一顆一顆的挑出來丟掉 就這樣丟掉了98顆球
現在主持人問你 要打開你一開始選擇的小盒子 還是他剛剛丟了98顆球的大箱子
如果你是在講開串的問題的話
不是文字遊戲 是個很經典的機率問題
我們換一個比喻來想像一下(數學上是一樣的)
情境是100選1
摸彩箱中有100顆球(材質、體積、重量、形狀等等都一樣,沒有做任何記號,除了用看的之外無法分辨不同)
裡面有1顆中獎球跟99顆未中獎
將這100顆球倒進一個無法觀測內部的箱子中
然後你現在把手伸進去用一個無法觀測內部的小盒子隨手裝了一顆球並把盒子鎖起來
接著把裝了一顆球的盒子拿出來之後放在旁邊
接下來 主持人在你取出一顆球的大箱子上面開了一個只有他能看到裡面的小開口
並把裡面的未中獎球一顆一顆的挑出來丟掉 就這樣丟掉了98顆球
現在主持人問你 要打開你一開始選擇的小盒子 還是他剛剛丟了98顆球的大箱子
>>2185633
車只有一台,你一開始選到車的機率是1/3
選到車之後無論主持人開哪一扇驢子門你一換都會輸,所以唯一的獲勝方式就是不換,這時的中獎率就跟選到車的機率一樣是1/3
驢子有兩頭,你一開始選到驢子的機率的2/3
因為主持人不能秀給你看車子在哪一道門後.所以不管哪你選到哪一頭驢子他一定得開剩下的另一個驢子門給你看
所以無論選到驢子A驢子B你只要一換一定就會換到還沒開的車子門
,這時的中獎率就會跟選到驢子一樣是2/3
你不換門最後會是三種結果,一種你贏(選車),兩種你輸(選驢子AB)
你換門最後一樣會是三種結果,兩種你贏(選驢子AB),一種你輸(選車子)
所以換門對你更有利!
車只有一台,你一開始選到車的機率是1/3
選到車之後無論主持人開哪一扇驢子門你一換都會輸,所以唯一的獲勝方式就是不換,這時的中獎率就跟選到車的機率一樣是1/3
驢子有兩頭,你一開始選到驢子的機率的2/3
因為主持人不能秀給你看車子在哪一道門後.所以不管哪你選到哪一頭驢子他一定得開剩下的另一個驢子門給你看
所以無論選到驢子A驢子B你只要一換一定就會換到還沒開的車子門
,這時的中獎率就會跟選到驢子一樣是2/3
你不換門最後會是三種結果,一種你贏(選車),兩種你輸(選驢子AB)
你換門最後一樣會是三種結果,兩種你贏(選驢子AB),一種你輸(選車子)
所以換門對你更有利!
>>2185639
如果看了上面的案例你還是聽不懂
那麼請把步驟先進行到取出一顆球封存放旁邊這裡
此時球被分在兩處
1.你從100顆球中隨機取出一顆封存的小盒子
2.一開始的100顆球被你取出1顆後剩下99顆球的大箱子
此時請問中獎球分別在小盒與大箱中的機率為何?
>小盒:1%
>大箱>99%
只要這個世界還遵循古典物理 沒有奇怪的量子波動介入這兩個容器
那麼無論主持人對大箱做甚麼事情 一開始被獨立封存的小盒就不會有所改變
無論主持人是要挑出98顆未中獎球 還是再扔一百顆進去大箱
"這整個大箱"中有中獎球的機率都是99%
小箱子是否有中獎球這件事情 在一開始挑出球並封存在小盒的當下就被固定了
如果看了上面的案例你還是聽不懂
那麼請把步驟先進行到取出一顆球封存放旁邊這裡
此時球被分在兩處
1.你從100顆球中隨機取出一顆封存的小盒子
2.一開始的100顆球被你取出1顆後剩下99顆球的大箱子
此時請問中獎球分別在小盒與大箱中的機率為何?
>小盒:1%
>大箱>99%
只要這個世界還遵循古典物理 沒有奇怪的量子波動介入這兩個容器
那麼無論主持人對大箱做甚麼事情 一開始被獨立封存的小盒就不會有所改變
無論主持人是要挑出98顆未中獎球 還是再扔一百顆進去大箱
"這整個大箱"中有中獎球的機率都是99%
小箱子是否有中獎球這件事情 在一開始挑出球並封存在小盒的當下就被固定了
>>2185641
我懂你想表達什麼,一樣的說法我看過了
但我覺得這是各種不同理論的其中一種解釋方法,並非是絕對唯一的正解
除非經過驗證,比方說換與不換各測試一百甚至一千次
如果換了的中獎次數真的比較高那我才服
我懂你想表達什麼,一樣的說法我看過了
但我覺得這是各種不同理論的其中一種解釋方法,並非是絕對唯一的正解
除非經過驗證,比方說換與不換各測試一百甚至一千次
如果換了的中獎次數真的比較高那我才服
無題 無名 21/01/13(三)02:40:20 ID:3HjvgjeE No.2185646
無題 無名 21/01/13(三)02:53:17 ID:3HjvgjeE No.2185649
>>2185644
如果你堅持換跟不換機率一樣的話
我這邊可以用稍微麻煩一點的方式來跟你在討論板隔空驗證機率
但樣本數少有比較大的可能性有偏差
因此我要求用100選1再牌除98個未中獎的方式運作
方法很簡單
1.我會上傳10個加密壓縮檔到雲端硬碟 分別標示01~10 代表每次驗證所使用的資料
2.那10個加密壓縮檔的內部是編號001~100隨機挑選一個數字的TXT檔案
3.你隨便選一個數字
4.我在知道哪個數字中獎的前提下 排除98個未中獎數字後留下你一開始選擇的數字與我提供的一個數字
5.你選擇是否要將選擇數字換成我後面提供的那個
6.我給你解壓縮密碼 你下載檔案後解壓縮確認中獎號碼
這樣可以用雲端硬碟的上傳時間紀錄做擔保我沒有作弊
請問要來試試看嗎?
如果你覺得太麻煩的話(我認真覺得挺麻煩的...)
你把同樣的方式用筆記本做小紙條紀錄一下找個朋友幫你測試就可以了
如果你堅持換跟不換機率一樣的話
我這邊可以用稍微麻煩一點的方式來跟你在討論板隔空驗證機率
但樣本數少有比較大的可能性有偏差
因此我要求用100選1再牌除98個未中獎的方式運作
方法很簡單
1.我會上傳10個加密壓縮檔到雲端硬碟 分別標示01~10 代表每次驗證所使用的資料
2.那10個加密壓縮檔的內部是編號001~100隨機挑選一個數字的TXT檔案
3.你隨便選一個數字
4.我在知道哪個數字中獎的前提下 排除98個未中獎數字後留下你一開始選擇的數字與我提供的一個數字
5.你選擇是否要將選擇數字換成我後面提供的那個
6.我給你解壓縮密碼 你下載檔案後解壓縮確認中獎號碼
這樣可以用雲端硬碟的上傳時間紀錄做擔保我沒有作弊
請問要來試試看嗎?
如果你覺得太麻煩的話(我認真覺得挺麻煩的...)
你把同樣的方式用筆記本做小紙條紀錄一下找個朋友幫你測試就可以了
最最簡單來說
換門就是在賭你一開始選到的是山羊
因為有兩個門是山羊
一開始選到山羊的機率比較高
= =
換門就是在賭你一開始選到的是山羊
因為有兩個門是山羊
一開始選到山羊的機率比較高
= =
無題 無名 21/01/13(三)03:30:06 ID:Oc0z1WAk No.2185653
>>2185652
...三小?
...三小?
無題 無名 21/01/13(三)03:38:16 ID:kl.kQdRg No.2185654
上面就講得很清楚了
只有三種可能
(1)你一開始就選中汽車 主持人給你看山羊A或B其中一隻 結果你換成了另一隻山羊
(2)你一開使選中山羊A 主持人給你看山羊B 結果你換成了汽車
(3)你一開使選中山羊B 主持人給你看山羊A 結果你換成了汽車
一開始選中汽車的機率比較低
要賭就要賭你一開始選的是山羊= =
只有三種可能
(1)你一開始就選中汽車 主持人給你看山羊A或B其中一隻 結果你換成了另一隻山羊
(2)你一開使選中山羊A 主持人給你看山羊B 結果你換成了汽車
(3)你一開使選中山羊B 主持人給你看山羊A 結果你換成了汽車
一開始選中汽車的機率比較低
要賭就要賭你一開始選的是山羊= =
無題 無名 21/01/13(三)04:12:23 ID:o5zGty62 No.2185657
無題 無名 21/01/13(三)08:31:50 ID:LeMfZGio No.2185668
>>2185644
所以你有實際試過嗎?
所以你有實際試過嗎?
>>2184877
我覺得你的算法怪怪的
機率是用C不是用P
你的可能性1明顯把山羊A跟B混為一談
看A選B如果照你的想法跟看B選A是一樣的
那你的選項2跟3應該要是同一個選項
所以機率應該是1/2
當主持人開了門
機率跟當初的本來就不一樣
然而換與不換都是一種選擇
只要主持人開了門
你的機率就從1/3進步到1/2
所以換不換沒有關係
因為你換跟不換都不會提升機率
我覺得你的算法怪怪的
機率是用C不是用P
你的可能性1明顯把山羊A跟B混為一談
看A選B如果照你的想法跟看B選A是一樣的
那你的選項2跟3應該要是同一個選項
所以機率應該是1/2
當主持人開了門
機率跟當初的本來就不一樣
然而換與不換都是一種選擇
只要主持人開了門
你的機率就從1/3進步到1/2
所以換不換沒有關係
因為你換跟不換都不會提升機率
無題 無名 21/01/13(三)10:17:38 ID:azh1/TA. No.2185689
>>2185643
錯
看上面不少人理解錯誤,我就一起說明
很多人似乎以為第一次門後有車的機率就是1/3
所以就算主持人開啟一扇有羊的門,門後有羊的機率仍不變
1-1/3=2/3
錯!
這兩個1/3指的完全是不同東西
第一次「門後有車」的機率確實是1/3
然而另一個1/3卻是指「不換門中車的機率」
當主持人開啟一扇有羊的門,此時剩餘兩扇門「門後有車」的機率都變成1/2
因此
>此時請問中獎球分別在小盒與大箱中的機率為何?
答案是各50%
99%是換盒子而有中獎球的機率
1%是不換盒子而有中獎球的機率
錯
看上面不少人理解錯誤,我就一起說明
很多人似乎以為第一次門後有車的機率就是1/3
所以就算主持人開啟一扇有羊的門,門後有羊的機率仍不變
1-1/3=2/3
錯!
這兩個1/3指的完全是不同東西
第一次「門後有車」的機率確實是1/3
然而另一個1/3卻是指「不換門中車的機率」
當主持人開啟一扇有羊的門,此時剩餘兩扇門「門後有車」的機率都變成1/2
因此
>此時請問中獎球分別在小盒與大箱中的機率為何?
答案是各50%
99%是換盒子而有中獎球的機率
1%是不換盒子而有中獎球的機率
無題 無名 21/01/13(三)10:42:34 ID:LeMfZGio No.2185699
>>2185696
只是複製了上面一個回應
(1)你一開始就選中汽車 主持人給你看山羊A或B其中一隻 結果你換成了另一隻山羊
(2)你一開使選中山羊A 主持人給你看山羊B 結果你換成了汽車
(3)你一開使選中山羊B 主持人給你看山羊A 結果你換成了汽車
以上,3門選1,只可能有3種結果
(1)你一開始就選中汽車
(2)你一開使選中山羊A
(3)你一開使選中山羊B
沒可能有其他結果,所以基數必然是3
看懂了嗎?AB羊一開始已經被分開計算
你的四種結果是反過來將車分開計了
只是複製了上面一個回應
(1)你一開始就選中汽車 主持人給你看山羊A或B其中一隻 結果你換成了另一隻山羊
(2)你一開使選中山羊A 主持人給你看山羊B 結果你換成了汽車
(3)你一開使選中山羊B 主持人給你看山羊A 結果你換成了汽車
以上,3門選1,只可能有3種結果
(1)你一開始就選中汽車
(2)你一開使選中山羊A
(3)你一開使選中山羊B
沒可能有其他結果,所以基數必然是3
看懂了嗎?AB羊一開始已經被分開計算
你的四種結果是反過來將車分開計了
>>2185708
那請問你擲筊結果幾種
機率怎麼算
那請問你擲筊結果幾種
機率怎麼算
無題 無名 21/01/13(三)11:00:09 ID:nx2OhQd6 No.2185710
>>2184712
這條討論到爛掉的概率問題居然是釣反智糞校生的魚餌嗎
這條討論到爛掉的概率問題居然是釣反智糞校生的魚餌嗎
選項一的A羊B羊是1/3選完門之後的事
選中A羊或B羊的機率各一半,所以最終兩種結果的機率是各1/6,合計1/3
選中A羊或B羊的機率各一半,所以最終兩種結果的機率是各1/6,合計1/3
無題 無名 21/01/13(三)11:05:54 ID:azh1/TA. No.2185718
>>2185713
你是來亂的吧?
你是來亂的吧?
無題 無名 21/01/13(三)11:08:01 ID:LeMfZGio No.2185721
不相信換是2/3的人肯做實驗了沒?
無題 無名 21/01/13(三)11:09:33 ID:azh1/TA. No.2185725
無題 無名 21/01/13(三)11:12:32 ID:1j/zuB8. No.2185727
>>2185706
那這樣有比較清楚嗎?
(1)你一開始就選中汽車 主持人給你看山羊A 結果你換成了山羊B
(2)你一開始就選中汽車 主持人給你看山羊B 結果你換成了山羊A
(3)你一開始選中山羊A 主持人給你看山羊B 結果你換成了汽車(4)你一開始選中山羊A 主持人原本要給你看汽車 可是這樣違反節目規定 所以換成讓你看山羊B 結果你換成了汽車
(5)你一開始選中山羊B 主持人給你看山羊A 結果你換成了汽車
(6)你一開始選中山羊B 主持人原本要給你看汽車 可是這樣違反節目規定 所以換成讓你看山羊A 結果你換成了汽車
選種山羊後,給你看汽車或另一隻山羊的機率應該是一樣的,但是主持人不可能讓你看汽車是前提,所以他會改成讓你看另一隻山羊
6個結果,兩個山羊 四個汽車
那這樣有比較清楚嗎?
(1)你一開始就選中汽車 主持人給你看山羊A 結果你換成了山羊B
(2)你一開始就選中汽車 主持人給你看山羊B 結果你換成了山羊A
(3)你一開始選中山羊A 主持人給你看山羊B 結果你換成了汽車(4)你一開始選中山羊A 主持人原本要給你看汽車 可是這樣違反節目規定 所以換成讓你看山羊B 結果你換成了汽車
(5)你一開始選中山羊B 主持人給你看山羊A 結果你換成了汽車
(6)你一開始選中山羊B 主持人原本要給你看汽車 可是這樣違反節目規定 所以換成讓你看山羊A 結果你換成了汽車
選種山羊後,給你看汽車或另一隻山羊的機率應該是一樣的,但是主持人不可能讓你看汽車是前提,所以他會改成讓你看另一隻山羊
6個結果,兩個山羊 四個汽車
無題 無名 21/01/13(三)11:13:16 ID:3HjvgjeE No.2185728
>>2185720
整個活動的起點是3扇門選1扇
羊不分AB的話就要把機率標出來 內容如下
世界線A 你選到車(機率1/3)
主持人要開一扇門炒熱氣氛
因為剩下的兩扇門都是羊 所以他可以隨意開一扇
接下來你換門的話就會選到羊
世界線B 你選到羊(機率2/3)
主持人要開一扇門炒熱氣氛
因為剩下的門有一車一羊 所以主持人必須選擇有羊的那扇門打開
接下來換門就賺一台車回家
整個活動的起點是3扇門選1扇
羊不分AB的話就要把機率標出來 內容如下
世界線A 你選到車(機率1/3)
主持人要開一扇門炒熱氣氛
因為剩下的兩扇門都是羊 所以他可以隨意開一扇
接下來你換門的話就會選到羊
世界線B 你選到羊(機率2/3)
主持人要開一扇門炒熱氣氛
因為剩下的門有一車一羊 所以主持人必須選擇有羊的那扇門打開
接下來換門就賺一台車回家
無題 無名 21/01/13(三)11:13:25 ID:duEcLL/w No.2185729
>>2185705
>如果沒有最初選擇,或者如果主持人隨便打開一扇門(可能主持人會直接開到汽車門,導致遊戲結束),又或者如果主持人只會在參賽者作出特定選擇某一門時才會問是否轉換選擇的話,問題都將會變得不一樣。例如,如果主持人先從兩隻山羊中剔除其中一隻,然後才叫參賽者作出選擇的話,選中的機會將會是1/2。
截自WIKI
自己看看好好了解
我說過很多次了
這個問題包含了「選門」以及「換門」兩個事件
>如果沒有最初選擇,或者如果主持人隨便打開一扇門(可能主持人會直接開到汽車門,導致遊戲結束),又或者如果主持人只會在參賽者作出特定選擇某一門時才會問是否轉換選擇的話,問題都將會變得不一樣。例如,如果主持人先從兩隻山羊中剔除其中一隻,然後才叫參賽者作出選擇的話,選中的機會將會是1/2。
截自WIKI
自己看看好好了解
我說過很多次了
這個問題包含了「選門」以及「換門」兩個事件
這篇會出現在歡樂惡搞的原因我終於理解了
因為經過了高達三百多篇的回應之後
還是有人試圖說服那些搞不懂的人
因為經過了高達三百多篇的回應之後
還是有人試圖說服那些搞不懂的人
無題 無名 21/01/13(三)11:25:35 ID:azh1/TA. No.2185736
>>2185735
原來是要惡搞想要解釋的人…可惡~中伏了…
原來是要惡搞想要解釋的人…可惡~中伏了…
無題 無名 21/01/13(三)11:31:08 ID:8XY54fPE No.2185738
其實把主持人換成指路人的角色就好了
小明在一個陌生的城市迷路了,來到一個十字路口,其中只有一個方向可以到他想去的目的地
這時一個當地人告訴他有兩個方位是絕對無法抵達的,只告訴他A路有可能會到他要去的地方
思考了一下之後,小明告訴這個指路人說...
「你肯定是想唬爛我的對吧,現在剩下兩條路,我走我最初選的路是1/2機率到達,我走你那條有可能的路也是1/2,這沒有差別吧」
指路人笑而不語,只是說小明肯定天生就很強運
小明在一個陌生的城市迷路了,來到一個十字路口,其中只有一個方向可以到他想去的目的地
這時一個當地人告訴他有兩個方位是絕對無法抵達的,只告訴他A路有可能會到他要去的地方
思考了一下之後,小明告訴這個指路人說...
「你肯定是想唬爛我的對吧,現在剩下兩條路,我走我最初選的路是1/2機率到達,我走你那條有可能的路也是1/2,這沒有差別吧」
指路人笑而不語,只是說小明肯定天生就很強運
>>2185731
你要搞清楚問題
題目問的是「換門後中車」的機率
但是當主持人挑出一隻羊,此時「門後有車」的機率就變成各是1/2
這兩者描述的事件是不同的
前者是一個連續事件,包含了選車及選擇要不要換車
後者只是獨立事件
不少人以為不換門中車機率1/3,是因為「這扇門」本來中車機率就是1/3,所以開啟一扇門後也不會變
然而並非如此
並不是因為中車機率不會變
而是因為,如果你不換門,本來中車的就會中車,本來不中車的就不會中車
會有這個1/3不是不換門之後,門後有車的機率,而是你一開始選到中獎門的機率
由於你選到中獎門不換門就一定中獎,所以是1/3*1=1/3
如果覺得這麼說很複雜,等我弄張圖表示
你要搞清楚問題
題目問的是「換門後中車」的機率
但是當主持人挑出一隻羊,此時「門後有車」的機率就變成各是1/2
這兩者描述的事件是不同的
前者是一個連續事件,包含了選車及選擇要不要換車
後者只是獨立事件
不少人以為不換門中車機率1/3,是因為「這扇門」本來中車機率就是1/3,所以開啟一扇門後也不會變
然而並非如此
並不是因為中車機率不會變
而是因為,如果你不換門,本來中車的就會中車,本來不中車的就不會中車
會有這個1/3不是不換門之後,門後有車的機率,而是你一開始選到中獎門的機率
由於你選到中獎門不換門就一定中獎,所以是1/3*1=1/3
如果覺得這麼說很複雜,等我弄張圖表示
無題 無名 21/01/13(三)11:52:23 ID:e42Iv4Ho No.2185746
無題 無名 21/01/13(三)11:58:32 ID:3HjvgjeE No.2185750
>>2185745
講機率聽不懂只能用絕招了...
所以你的論點是換跟不換都是50%機率嗎?
如果是的話 我可以幫你出車馬費
可以到我指定地點跟我賭一下錢嗎?
3門問題 100局
你只能選擇不換門
你選中了 我每次給你1500元
你沒選中 你每次給我1000元
機率50%的話每兩次平均你可以賺500元
來一趟就可以賺500*50=25000元了
這麼好賺的機會你要不要來?
講機率聽不懂只能用絕招了...
所以你的論點是換跟不換都是50%機率嗎?
如果是的話 我可以幫你出車馬費
可以到我指定地點跟我賭一下錢嗎?
3門問題 100局
你只能選擇不換門
你選中了 我每次給你1500元
你沒選中 你每次給我1000元
機率50%的話每兩次平均你可以賺500元
來一趟就可以賺500*50=25000元了
這麼好賺的機會你要不要來?
無題 無名 21/01/13(三)12:15:20 ID:3HjvgjeE No.2185752
面對面各方面成本都有點高 剛才找了一個線上加密網站
https://www.ifreesite.com/textencrypt/
我這邊先對15個數字(1~3隨機)進行了加密 加密後的字串為
U2FsdGVkX18eVJIg6jTrSBOPeRZIS8H0/zU1rmikZjSyeayHj1sNyyZZPuMlK/3m
因為有設密碼所以現在無法直接解密
有人要來實測嗎?
很簡單 給我1~3個數字15個就好
接下來我會排除掉一個非中獎數字後讓你再度選擇是否換號碼
選完之後我會公開上面自串的密碼供解密翻解答
https://www.ifreesite.com/textencrypt/
我這邊先對15個數字(1~3隨機)進行了加密 加密後的字串為
U2FsdGVkX18eVJIg6jTrSBOPeRZIS8H0/zU1rmikZjSyeayHj1sNyyZZPuMlK/3m
因為有設密碼所以現在無法直接解密
有人要來實測嗎?
很簡單 給我1~3個數字15個就好
接下來我會排除掉一個非中獎數字後讓你再度選擇是否換號碼
選完之後我會公開上面自串的密碼供解密翻解答
>>2185745
也不是這麼說
這個題目是「換門後中車的機率」
正確說法是「選擇一扇門,換門後中車的機率」
所以先不談機率多少
要先分析「選擇一扇門」中車與否對換門與否的影響
1.從主持人會開啟一扇有羊的門來看,場上只會剩下2扇門中與不中
2.由於只剩2扇中與不中的門,原本中的換了會不中,不換則是會中,原本不中的一樣道理
因此,倘若要「不換門中車」
就能從結果逆推,要找出原本就中車的門,也就是1/3
所以呢~應該說在換門或不換門的前提下,第一次選擇就已經決定了這事件的機率
因為3扇門在刪去一扇門後只剩中與不中2扇門,省略掉很多東西,所以會有一種錯覺
我上面有舉例5門4羊1車,選擇一扇門後開啟一扇有羊的門
當你一開始選到有羊的門,即便換門仍有機會還是選到羊,這樣來看整體就會清楚許多
也不是這麼說
這個題目是「換門後中車的機率」
正確說法是「選擇一扇門,換門後中車的機率」
所以先不談機率多少
要先分析「選擇一扇門」中車與否對換門與否的影響
1.從主持人會開啟一扇有羊的門來看,場上只會剩下2扇門中與不中
2.由於只剩2扇中與不中的門,原本中的換了會不中,不換則是會中,原本不中的一樣道理
因此,倘若要「不換門中車」
就能從結果逆推,要找出原本就中車的門,也就是1/3
所以呢~應該說在換門或不換門的前提下,第一次選擇就已經決定了這事件的機率
因為3扇門在刪去一扇門後只剩中與不中2扇門,省略掉很多東西,所以會有一種錯覺
我上面有舉例5門4羊1車,選擇一扇門後開啟一扇有羊的門
當你一開始選到有羊的門,即便換門仍有機會還是選到羊,這樣來看整體就會清楚許多
無題 無名 21/01/13(三)12:20:00 ID:In17r2h. No.2185757
>>2185745
第一次的選擇當然有差
你是在未知門後物品的情況下三選一
可能的情況有車、羊A、羊B 故得到車的機率是1/3
如果你決定堅持不換的話 那無論主持人掀不掀門你得到車的機率一樣只有1/3
因為你第一次選擇是在“三扇門皆未知時選擇其中一扇門“與“兩扇門皆未知時選一扇門“是完全不一樣的狀況
你的選擇是“1/3得到車的選擇“ 堅持不換不會提高中獎機率的懂嗎?
第一次的選擇當然有差
你是在未知門後物品的情況下三選一
可能的情況有車、羊A、羊B 故得到車的機率是1/3
如果你決定堅持不換的話 那無論主持人掀不掀門你得到車的機率一樣只有1/3
因為你第一次選擇是在“三扇門皆未知時選擇其中一扇門“與“兩扇門皆未知時選一扇門“是完全不一樣的狀況
你的選擇是“1/3得到車的選擇“ 堅持不換不會提高中獎機率的懂嗎?
>>2185764
我反覆研究你說的那堆鬼東西之後
終於理解為什麼你可以堅持自己正確又說出一堆亂七八糟的內容了
這題目的重點一直都是在全部題目內的情報都清楚的狀況下去判斷門後面的機率
你所謂的50/50機率 只存在於 排除一開始選擇步驟的情報 直接展示兩扇門要進行選擇的狀況
但這個狀況從頭到尾都不是這題目要問的東西
在獲取同樣情報的前提下 並不會因為你是遊戲的參與者或者旁邊的觀眾而有不同的機率模型
我覺得你需要重新把你的表達思路整理清楚 這串正在大混戰中
你或許可以考慮在現實世界隨便找個朋友討論 並試著講解說明看看
我反覆研究你說的那堆鬼東西之後
終於理解為什麼你可以堅持自己正確又說出一堆亂七八糟的內容了
這題目的重點一直都是在全部題目內的情報都清楚的狀況下去判斷門後面的機率
你所謂的50/50機率 只存在於 排除一開始選擇步驟的情報 直接展示兩扇門要進行選擇的狀況
但這個狀況從頭到尾都不是這題目要問的東西
在獲取同樣情報的前提下 並不會因為你是遊戲的參與者或者旁邊的觀眾而有不同的機率模型
我覺得你需要重新把你的表達思路整理清楚 這串正在大混戰中
你或許可以考慮在現實世界隨便找個朋友討論 並試著講解說明看看
>>2185762
然後我再補一句
你有換門這個過程就是你要先選門
如果你說「換門後中車的機率」是1/2
就是無視了你之前有選門,所以也根本不存在換門後這件事
單純只計算『門後中車』的這件事,所以認為只有中和不中的1/2
這就是我說的原PO片中說的掉進1/2陷阱的人…
這年頭是不是不懂的人就比較大聲?
然後我再補一句
你有換門這個過程就是你要先選門
如果你說「換門後中車的機率」是1/2
就是無視了你之前有選門,所以也根本不存在換門後這件事
單純只計算『門後中車』的這件事,所以認為只有中和不中的1/2
這就是我說的原PO片中說的掉進1/2陷阱的人…
這年頭是不是不懂的人就比較大聲?
>>2185778
條件機率這個東西已經提過很多次了
不同的條件就會有不同的機率模型
我真的不知道你是中文還是數學有問題了......
你可以把你的高見發表給你身旁的朋友看看
不管他是不是數學系的 我相信不是聽不懂你在供三小就是瘋狂吐槽你
條件機率這個東西已經提過很多次了
不同的條件就會有不同的機率模型
我真的不知道你是中文還是數學有問題了......
你可以把你的高見發表給你身旁的朋友看看
不管他是不是數學系的 我相信不是聽不懂你在供三小就是瘋狂吐槽你
無題 無名 21/01/13(三)13:10:29 ID:duEcLL/w No.2185785
>>2185781
是你們搞不懂我在說什麼
1.門後有車的機率
2.換門後中車的機率
我說的是前者機率的確變成1/2
然而有些不懂裝懂的人卻以為機率不會變,還是1/3,並以此來解釋答案
然而人家要的是換門後中車的機率
別再鬼打牆了好嗎
是你們搞不懂我在說什麼
1.門後有車的機率
2.換門後中車的機率
我說的是前者機率的確變成1/2
然而有些不懂裝懂的人卻以為機率不會變,還是1/3,並以此來解釋答案
然而人家要的是換門後中車的機率
別再鬼打牆了好嗎
>>2185782
"在所有情報已知的前提下"
假設ABC三門
一開始選擇A門
主持人開掉B門
都沒人動的C門
現在剩下兩扇門AC
初始ABC三門機率皆為1/3
雖然你想主張的是主持人將B門開掉之後
AC門的機率皆為1/2
但由於題目的條件限制 會將B門的機率收斂至C門
A門=不換門=1/3中獎
C門=換門=2/3中獎
我覺得你應該是有一部份理解但又有一部份的邏輯卡住了
才會出現那種同時有1/2又有1/3的機率存在於同一扇門的奇怪量子態......
"在所有情報已知的前提下"
假設ABC三門
一開始選擇A門
主持人開掉B門
都沒人動的C門
現在剩下兩扇門AC
初始ABC三門機率皆為1/3
雖然你想主張的是主持人將B門開掉之後
AC門的機率皆為1/2
但由於題目的條件限制 會將B門的機率收斂至C門
A門=不換門=1/3中獎
C門=換門=2/3中獎
我覺得你應該是有一部份理解但又有一部份的邏輯卡住了
才會出現那種同時有1/2又有1/3的機率存在於同一扇門的奇怪量子態......
我再說一遍
「換門後中車」的機率是2/3
但之所以是2/3,是因為換門這一行為會讓「原本中車的變成不中車」、「原本不中車的變成中車」
而原本不中車的機率是2/3,因此就會變成「換門後中車的機率是2/3」
而有些不懂裝懂的人會認為,選定一個門,這個門原本中車的機率是1/3,所以「主持人開啟一扇門後,中車的機率也不會變」,一樣是1/3
1-1/3=2/3
這完全就是錯誤
不只對題目理解錯誤,連最後求到的機率都是錯誤
我知道你們想表現那種自己很厲害的優越感
看到別人說出1/2就會大叫錯誤
但是至少先把別人的文章看完,了解人家說什麼再來討論好嗎
你們還在檢討答案是1/2或2/3
我是在糾正得出2/3這個答案的錯誤方式
「換門後中車」的機率是2/3
但之所以是2/3,是因為換門這一行為會讓「原本中車的變成不中車」、「原本不中車的變成中車」
而原本不中車的機率是2/3,因此就會變成「換門後中車的機率是2/3」
而有些不懂裝懂的人會認為,選定一個門,這個門原本中車的機率是1/3,所以「主持人開啟一扇門後,中車的機率也不會變」,一樣是1/3
1-1/3=2/3
這完全就是錯誤
不只對題目理解錯誤,連最後求到的機率都是錯誤
我知道你們想表現那種自己很厲害的優越感
看到別人說出1/2就會大叫錯誤
但是至少先把別人的文章看完,了解人家說什麼再來討論好嗎
你們還在檢討答案是1/2或2/3
我是在糾正得出2/3這個答案的錯誤方式
>>2185782
看你腦卡住了
3門選門換門是既定事實,是一個母體,此後的都不能獨立計算
因此
1.門後有車的機率(1/3)
2.換門後中車的機率(2/3)
都不是1/2
所以只要把最後結果理解成1/2者,都是中陷阱
看你腦卡住了
3門選門換門是既定事實,是一個母體,此後的都不能獨立計算
因此
1.門後有車的機率(1/3)
2.換門後中車的機率(2/3)
都不是1/2
所以只要把最後結果理解成1/2者,都是中陷阱
>>2185791
>選定一個門,這個門原本中車的機率是1/3,所以「主持人開啟一扇門後,中車的機率也不會變」,一樣是1/3
>1-(1/3)=(2/3)
這段論述完全正確(我多加了括弧讓他看起來清楚一點)
實際上這段話跟你所謂的正確邏輯在數學上是一樣的
只是從從不同的方向作推導而已
看來你是用一個方式理解 認定這就是正確解答之後就無法理解其他路徑的人呢......
>選定一個門,這個門原本中車的機率是1/3,所以「主持人開啟一扇門後,中車的機率也不會變」,一樣是1/3
>1-(1/3)=(2/3)
這段論述完全正確(我多加了括弧讓他看起來清楚一點)
實際上這段話跟你所謂的正確邏輯在數學上是一樣的
只是從從不同的方向作推導而已
看來你是用一個方式理解 認定這就是正確解答之後就無法理解其他路徑的人呢......
不然這樣好了
想像一下你面前有張一百題的考卷
每題都是三選一的單選題
而且助教跟你說答案中ABC三個選項大約是平均分佈
雖然你沒念書所以一題都看不懂
但天才如你就想
既然選項平均分佈
那全部亂猜也會有大概33分才對
1/3機率猜中嘛
不過助教看到你這麼慘
打算給你一些提示
所以他就把你的考卷上每一題裡
劃掉一個你沒有選的選項
跟你說那個不是答案
你要不要再花點時間
換到另外一個你沒選的選項
然後天才如你又想了
本來三選一機率是1/3,大概會拿到33分
現在只剩下兩個選項,所以機率一定會變成1/2,大概能拿到50分
雖然每一題的正確答案早就定好了
雖然你考卷上的作答通通沒改過
但你還是相信在助教幫你劃掉一個選項,從三個變成兩個的那瞬間
就算你不更改任何一題作答
你考卷的分數就會從大概33分忽然變成大概50分
你說,天底下有這麼神奇的事情嗎?
想像一下你面前有張一百題的考卷
每題都是三選一的單選題
而且助教跟你說答案中ABC三個選項大約是平均分佈
雖然你沒念書所以一題都看不懂
但天才如你就想
既然選項平均分佈
那全部亂猜也會有大概33分才對
1/3機率猜中嘛
不過助教看到你這麼慘
打算給你一些提示
所以他就把你的考卷上每一題裡
劃掉一個你沒有選的選項
跟你說那個不是答案
你要不要再花點時間
換到另外一個你沒選的選項
然後天才如你又想了
本來三選一機率是1/3,大概會拿到33分
現在只剩下兩個選項,所以機率一定會變成1/2,大概能拿到50分
雖然每一題的正確答案早就定好了
雖然你考卷上的作答通通沒改過
但你還是相信在助教幫你劃掉一個選項,從三個變成兩個的那瞬間
就算你不更改任何一題作答
你考卷的分數就會從大概33分忽然變成大概50分
你說,天底下有這麼神奇的事情嗎?
無題 無名 21/01/13(三)13:42:42 ID:3AVBjL2k No.2185798
>>2185791
>選定一個門,這個門原本中車的機率是1/3,所以「主持人開啟一扇門後,中車的機率也不會變」,一樣是1/3
由於選門是一開始3選1,一定就是1/3不變
之後不論主持人開啟不開一扇門,1/3這機率也不會變
並不會因為選門之後主持人再開啟一扇門,1/3中車的機率就會改變
反而為什麼你會認為主持人開啟一扇門後,中車的機率會變?
>選定一個門,這個門原本中車的機率是1/3,所以「主持人開啟一扇門後,中車的機率也不會變」,一樣是1/3
由於選門是一開始3選1,一定就是1/3不變
之後不論主持人開啟不開一扇門,1/3這機率也不會變
並不會因為選門之後主持人再開啟一扇門,1/3中車的機率就會改變
反而為什麼你會認為主持人開啟一扇門後,中車的機率會變?
>>2185787
>>2185792
>如果沒有最初選擇,或者如果主持人隨便打開一扇門(可能主持人會直接開到汽車門,導致遊戲結束),又或者如果主持人只會在參賽者作出特定選擇某一門時才會問是否轉換選擇的話,問題都將會變得不一樣。例如,如果主持人先從兩隻山羊中剔除其中一隻,然後才叫參賽者作出選擇的話,選中的機會將會是1/2。
>例如,如果主持人先從兩隻山羊中剔除其中一隻,然後才叫參賽者作出選擇的話,選中的機會將會是1/2。
拿這舉例來說明
假設同樣是三扇門,但是一開不要你選擇
請問每扇門後有車的機率是多少?
答案很明瞭的是1/3吧
然後主持人打開一扇有羊的門,才叫你選擇
依照你的說法,門後有車的機率不會變,還會是1/3
然而正解是1/2
你們最大的問題就是從答案回推過程
但是卻沒有正確理解
>>2185792
>如果沒有最初選擇,或者如果主持人隨便打開一扇門(可能主持人會直接開到汽車門,導致遊戲結束),又或者如果主持人只會在參賽者作出特定選擇某一門時才會問是否轉換選擇的話,問題都將會變得不一樣。例如,如果主持人先從兩隻山羊中剔除其中一隻,然後才叫參賽者作出選擇的話,選中的機會將會是1/2。
>例如,如果主持人先從兩隻山羊中剔除其中一隻,然後才叫參賽者作出選擇的話,選中的機會將會是1/2。
拿這舉例來說明
假設同樣是三扇門,但是一開不要你選擇
請問每扇門後有車的機率是多少?
答案很明瞭的是1/3吧
然後主持人打開一扇有羊的門,才叫你選擇
依照你的說法,門後有車的機率不會變,還會是1/3
然而正解是1/2
你們最大的問題就是從答案回推過程
但是卻沒有正確理解
無題 無名 21/01/13(三)14:09:37 ID:duEcLL/w No.2185811
>>2185794
別瞎扯
根本不一樣好嗎
你這完全就是搞混「門後有車」和「換門後中車」兩件事
我上面說過好多次了
今天假設一個人從後半開始看,他只知道一扇開啟的門有羊,其他兩扇是一羊一車,對他來說選中車(也就是門後有車)的機率是1/2
你會覺得機率不變完全是逆推答案的誤解
主持人開啟一扇門後,你選中車(也就是門後有車)的機率就變成1/2
但我也說過,這和題目不相關
題目要的是換門後中車的機率
多數人會回答1/2就是沒搞清楚兩者的差異,也可以說是種文字陷阱
而會用這種錯誤思維來推答案的人,也幾乎能肯定是最初用這種想法答1/2的人
別瞎扯
根本不一樣好嗎
你這完全就是搞混「門後有車」和「換門後中車」兩件事
我上面說過好多次了
今天假設一個人從後半開始看,他只知道一扇開啟的門有羊,其他兩扇是一羊一車,對他來說選中車(也就是門後有車)的機率是1/2
你會覺得機率不變完全是逆推答案的誤解
主持人開啟一扇門後,你選中車(也就是門後有車)的機率就變成1/2
但我也說過,這和題目不相關
題目要的是換門後中車的機率
多數人會回答1/2就是沒搞清楚兩者的差異,也可以說是種文字陷阱
而會用這種錯誤思維來推答案的人,也幾乎能肯定是最初用這種想法答1/2的人
>>2185806
>1.門後有車的機率(1/3)
你自己說的
門後有車的機率並不會被你是否有選門影響
也就是說一開始是否有選車和門後有車的機率無關
因此
一開始選門,主持人開啟一扇有羊的門,其他兩扇門門後有車的機率
與
一開始沒選門,主持人開啟一扇有羊的門,其他兩扇門門後有車的機率
是一樣的
>1.門後有車的機率(1/3)
你自己說的
門後有車的機率並不會被你是否有選門影響
也就是說一開始是否有選車和門後有車的機率無關
因此
一開始選門,主持人開啟一扇有羊的門,其他兩扇門門後有車的機率
與
一開始沒選門,主持人開啟一扇有羊的門,其他兩扇門門後有車的機率
是一樣的
無題 無名 21/01/13(三)14:22:12 ID:duEcLL/w No.2185817
>>2185814
由於選門是一開始3選1,一定就是1/3不變
之後不論主持人開啟不開一扇門,1/3這機率也不會變
並不會因為選門之後主持人再開啟一扇門,1/3中車的機率就會改變
選門是一開始3選1,「選門之後」不論主持人開啟不開一扇門
選門是一開始3選1,「選門之後」不論主持人開啟不開一扇門
選門是一開始3選1,「選門之後」不論主持人開啟不開一扇門
你眼睛跟理解力都沒問題吧
由於選門是一開始3選1,一定就是1/3不變
之後不論主持人開啟不開一扇門,1/3這機率也不會變
並不會因為選門之後主持人再開啟一扇門,1/3中車的機率就會改變
選門是一開始3選1,「選門之後」不論主持人開啟不開一扇門
選門是一開始3選1,「選門之後」不論主持人開啟不開一扇門
選門是一開始3選1,「選門之後」不論主持人開啟不開一扇門
你眼睛跟理解力都沒問題吧
>>2185818
不懂就不要裝懂,去查資料或問老師
你一開始是3選1,3扇門後有車的機率各是1/3
但是開啟一扇有羊的門之後,就變成2選1,2扇門後有車的機率各是1/2
不影響門後有車機率的是選不選門,不是開不開門
你那個1/3是因為一開始選中中車的門機率是1/3,然後不換門必中所以機率是1,1/3*1=1/3
兩者描述的事件不同
你把門後有車的機率當成是不換門中車的機率就像拿300日圓去買300台幣的東西
不懂就不要裝懂,去查資料或問老師
你一開始是3選1,3扇門後有車的機率各是1/3
但是開啟一扇有羊的門之後,就變成2選1,2扇門後有車的機率各是1/2
不影響門後有車機率的是選不選門,不是開不開門
你那個1/3是因為一開始選中中車的門機率是1/3,然後不換門必中所以機率是1,1/3*1=1/3
兩者描述的事件不同
你把門後有車的機率當成是不換門中車的機率就像拿300日圓去買300台幣的東西
無題 無名 21/01/13(三)14:47:57 ID:duEcLL/w No.2185823
>>2185818
如果很難理解
那我舉高中數學最愛的取球問題當例子
一個袋子有4個白球、6個黑球
1.請問從袋子中取出一個球是白球的機率是多少?
2.再請問,從袋子中拿走一個黑球,這時候取出一個球是白球的機率是否和題1.相同?
如果很難理解
那我舉高中數學最愛的取球問題當例子
一個袋子有4個白球、6個黑球
1.請問從袋子中取出一個球是白球的機率是多少?
2.再請問,從袋子中拿走一個黑球,這時候取出一個球是白球的機率是否和題1.相同?
>>2185827
兩者根本是不可能獨立描述的事件
開啟一扇有羊的門之後,就像變成2選1,但這是建基於你先前己3選1之後,故你折手中的門依然是1/3
雖然你現在手中門依然是1/3
就不可能這2扇門後有車的機率各是1/2
先選後開跟先開後選,是兩個完全不同的情況
聽你這樣,你是錯誤理解成,選門後開門,等於從一開始就有一個羊門被刪除
兩者根本是不可能獨立描述的事件
開啟一扇有羊的門之後,就像變成2選1,但這是建基於你先前己3選1之後,故你折手中的門依然是1/3
雖然你現在手中門依然是1/3
就不可能這2扇門後有車的機率各是1/2
先選後開跟先開後選,是兩個完全不同的情況
聽你這樣,你是錯誤理解成,選門後開門,等於從一開始就有一個羊門被刪除
>>2185825
我特地去看了英文,結果題目應該是「玩家是換門而中車的機率高,還是不換門而中車的機率高」
然後我把所有可能發生的情況,用文字重新列出來每一條,終於理解為什麼會有人覺得機率不變動了
假設有3個門,編號1、2、3
3號後面有車,不過玩家不知道
主持知道3號後面有車,在玩家第一次選門之後,主持會從剩下2個門中間開1扇,且「必定不會開有車的那扇」
所有可能發生的情況應該是這8種
玩家選1,主持開2,玩家不換門繼續開1>沒中
玩家選1,主持開2,玩家要換門改成開3>中
玩家選2,主持開1,玩家不換門繼續開2>沒中
玩家選2,主持開1,玩家要換門改成開3>中
玩家選3,主持開1,玩家不換門繼續開3>中
玩家選3,主持開1,玩家要換門改成開2>沒中
玩家選3,主持開2,玩家不換門繼續開3>中
玩家選3,主持開2,玩家要換門改成開1>沒中
我特地去看了英文,結果題目應該是「玩家是換門而中車的機率高,還是不換門而中車的機率高」
然後我把所有可能發生的情況,用文字重新列出來每一條,終於理解為什麼會有人覺得機率不變動了
假設有3個門,編號1、2、3
3號後面有車,不過玩家不知道
主持知道3號後面有車,在玩家第一次選門之後,主持會從剩下2個門中間開1扇,且「必定不會開有車的那扇」
所有可能發生的情況應該是這8種
玩家選1,主持開2,玩家不換門繼續開1>沒中
玩家選1,主持開2,玩家要換門改成開3>中
玩家選2,主持開1,玩家不換門繼續開2>沒中
玩家選2,主持開1,玩家要換門改成開3>中
玩家選3,主持開1,玩家不換門繼續開3>中
玩家選3,主持開1,玩家要換門改成開2>沒中
玩家選3,主持開2,玩家不換門繼續開3>中
玩家選3,主持開2,玩家要換門改成開1>沒中
無題 無名 21/01/13(三)15:13:55 ID:duEcLL/w No.2185832
>>2185828
他認為因為一開始選到有車的門機率是1/3,所以就算開啟一扇門,這扇門有車的機率還是1/3
我則是舉例給他看
不管你一開始有沒有選門,這3扇門有車的機率都是1/3,而開啟一扇門之後,有車的機率就會變成2選1的1/2
因為他誤解了「換門與否中車的機率」和「這扇門後有車的機率」
然後發問前可不可以先拉上去看在討論什麼啊
他認為因為一開始選到有車的門機率是1/3,所以就算開啟一扇門,這扇門有車的機率還是1/3
我則是舉例給他看
不管你一開始有沒有選門,這3扇門有車的機率都是1/3,而開啟一扇門之後,有車的機率就會變成2選1的1/2
因為他誤解了「換門與否中車的機率」和「這扇門後有車的機率」
然後發問前可不可以先拉上去看在討論什麼啊
>>2185830
說真的
你到底能不能分辨「門後有車」的機率和「換門後中車」的機率
我覺得你一直沒搞懂我在說什麼
在這個題目,「門後有車」的機率和「換門後中車」的機率沒有直接關係
我會拿出「門後有車」的機率來說是因為有人用錯誤的方式來解題,以為兩者是有關聯的
然後我覺得你的說法問題很大
>開啟一扇有羊的門之後,就像變成2選1,但這是建基於你先前已3選1之後
正確
>故你折手中的門依然是1/3
這個1/3是你不換門中車的機率,並非這扇門後面是車的機率
>就不可能這2扇門後有車的機率各是1/2
錯誤,描述的對象錯誤
因為在之前就選過門了,所以「對你來說」不換門中車的機率是1/3,這是對你這個做選擇的人來說
然而,「對門來說」,這扇門後是車或羊的機率各是1/2
我上面有舉取球問題當例子,去看一下就知道問題在哪
說真的
你到底能不能分辨「門後有車」的機率和「換門後中車」的機率
我覺得你一直沒搞懂我在說什麼
在這個題目,「門後有車」的機率和「換門後中車」的機率沒有直接關係
我會拿出「門後有車」的機率來說是因為有人用錯誤的方式來解題,以為兩者是有關聯的
然後我覺得你的說法問題很大
>開啟一扇有羊的門之後,就像變成2選1,但這是建基於你先前已3選1之後
正確
>故你折手中的門依然是1/3
這個1/3是你不換門中車的機率,並非這扇門後面是車的機率
>就不可能這2扇門後有車的機率各是1/2
錯誤,描述的對象錯誤
因為在之前就選過門了,所以「對你來說」不換門中車的機率是1/3,這是對你這個做選擇的人來說
然而,「對門來說」,這扇門後是車或羊的機率各是1/2
我上面有舉取球問題當例子,去看一下就知道問題在哪
無題 無名 21/01/13(三)15:40:33 ID:T01.7NTc No.2185839
哇......這串還在繼續喔
是在造福目前是學生的人嗎? 大家加油
不過如果不是學生就算了吧 反正一般人懂不懂又沒差
會深入到更高層級應用的也不會拘泥在這種小問題上
是在造福目前是學生的人嗎? 大家加油
不過如果不是學生就算了吧 反正一般人懂不懂又沒差
會深入到更高層級應用的也不會拘泥在這種小問題上
無題 無名 21/01/13(三)16:05:10 ID:duEcLL/w No.2185843
我知道有些人大概是看到回答過程出現1/2就急著出來喊錯
但是如果把題目放大到5門4羊1車,選一扇門又開啟一扇有羊的門,就會了解並非全然不相關
在這個問題中,和3扇門一樣,倘若你一開始選到中車的門,換門勢必會不中
所以選到中車的門又換門的中車機是1/5*0=0
然而,如果你一開始選到不中的門,就算換門也不見得會中車
問題來了,假設你真的堅持門後有車的機率不會變,那可能就會進入死胡同
你一開始選了不中的門,主持人又開啟一扇不中的門,剩下的3扇門中只有一扇是中的
因此在「確定你已經選擇不中的門」這一條件下,換門中車的機率是1/3
只是「換門中車的機率」並沒有設下第一次選擇是否中車的條件
所以答案要同時計算
一開始選到中車的門,換門後中車
與
一開始選到不中的門,換門後中車
的機率
即是(1/5*0)+(4/5*1/3)=4/15
但是如果把題目放大到5門4羊1車,選一扇門又開啟一扇有羊的門,就會了解並非全然不相關
在這個問題中,和3扇門一樣,倘若你一開始選到中車的門,換門勢必會不中
所以選到中車的門又換門的中車機是1/5*0=0
然而,如果你一開始選到不中的門,就算換門也不見得會中車
問題來了,假設你真的堅持門後有車的機率不會變,那可能就會進入死胡同
你一開始選了不中的門,主持人又開啟一扇不中的門,剩下的3扇門中只有一扇是中的
因此在「確定你已經選擇不中的門」這一條件下,換門中車的機率是1/3
只是「換門中車的機率」並沒有設下第一次選擇是否中車的條件
所以答案要同時計算
一開始選到中車的門,換門後中車
與
一開始選到不中的門,換門後中車
的機率
即是(1/5*0)+(4/5*1/3)=4/15
無題 無名 21/01/13(三)16:06:29 ID:4oFrCVSU No.2185845
>>2185831
承上,但是我們把會中車的情況抽出來
玩家選1開3>有換,中
玩家選2開3>有換,中
玩家選3開3>沒換,中
只有這3種,所以回到題目「玩家是換門而中車的機率高,還是不換門而中車的機率高」
答案是「玩家有換門而中車的機率高」
承上,但是我們把會中車的情況抽出來
玩家選1開3>有換,中
玩家選2開3>有換,中
玩家選3開3>沒換,中
只有這3種,所以回到題目「玩家是換門而中車的機率高,還是不換門而中車的機率高」
答案是「玩家有換門而中車的機率高」
無題 無名 21/01/13(三)16:06:35 ID:6ueRCIcM No.2185846
>>2185617
>要是三個門後面分別是
>[史上最貴的名牌車+永久保固]
>[一團黑影附加許多眼睛跟黑色的手]
>[一群人圍著你鼓掌拍手並說おめでとう]
這樣不平等拉
第一門要改成[一台靠垃圾當燃料並且可以穿越時空的車子]
>要是三個門後面分別是
>[史上最貴的名牌車+永久保固]
>[一團黑影附加許多眼睛跟黑色的手]
>[一群人圍著你鼓掌拍手並說おめでとう]
這樣不平等拉
第一門要改成[一台靠垃圾當燃料並且可以穿越時空的車子]
無題 無名 21/01/13(三)16:11:33 ID:gP2tldOw No.2185849
>>2185838
所以就說沒有「對門來說」是1/2這種事,因為先3選門己經既然了機率
即是你的門1/3,主持人的2門2/3,主持人只是之後刪去了1門,主持人的門一樣是2/3
所以2扇門後有車的機率各是你的門是1/3,主持人的門是2/3
你換就是換成2/3
不換是1/3
機率不能這樣在連續事件中獨立算的
所以你在這連續事件中單純就「對門來說」門後有車的機率是1/2是個錯誤描述
沒有「對門來說」這樣再算一個不同的機率出來這回事
你這車或羊的機率各是1/2
只可能是先前不是3選1才能成立
所以就說沒有「對門來說」是1/2這種事,因為先3選門己經既然了機率
即是你的門1/3,主持人的2門2/3,主持人只是之後刪去了1門,主持人的門一樣是2/3
所以2扇門後有車的機率各是你的門是1/3,主持人的門是2/3
你換就是換成2/3
不換是1/3
機率不能這樣在連續事件中獨立算的
所以你在這連續事件中單純就「對門來說」門後有車的機率是1/2是個錯誤描述
沒有「對門來說」這樣再算一個不同的機率出來這回事
你這車或羊的機率各是1/2
只可能是先前不是3選1才能成立
>>2185842
100扇門開啟98扇有羊的門
最終兩扇門門後有車的機率一樣是1/2
要「換門中車」的機率才不是1/2
舉例來說
你以為的情況是這樣
一個袋子有1顆白球和99顆黑球
現在你抽出一顆球是白球的機率是1/100
但是如果我拿出98顆黑球再讓你抽呢?你還會說抽出一顆球是白球的機率是1/100嗎?
而三門問題的情況是這樣
一個袋子有1顆白球和99顆黑球
現在讓你伸手進去選一顆球握住,我把其他98顆黑球取走
然後問你,把手中的球換成另一顆,是白球的機率是多少
因為你剛剛有99/100的機率握住黑球,只要剛剛握住的是黑球,交換就會變成白球,所以才會有99/100的機率換得白球
100扇門開啟98扇有羊的門
最終兩扇門門後有車的機率一樣是1/2
要「換門中車」的機率才不是1/2
舉例來說
你以為的情況是這樣
一個袋子有1顆白球和99顆黑球
現在你抽出一顆球是白球的機率是1/100
但是如果我拿出98顆黑球再讓你抽呢?你還會說抽出一顆球是白球的機率是1/100嗎?
而三門問題的情況是這樣
一個袋子有1顆白球和99顆黑球
現在讓你伸手進去選一顆球握住,我把其他98顆黑球取走
然後問你,把手中的球換成另一顆,是白球的機率是多少
因為你剛剛有99/100的機率握住黑球,只要剛剛握住的是黑球,交換就會變成白球,所以才會有99/100的機率換得白球
無題 無名 21/01/13(三)16:35:28 ID:duEcLL/w No.2185855
>>2185851
你的腦袋真的比石頭還硬
我就和你說那是不同事件了,因為你把兩者混為一談我才同時提到
你根本沒搞清楚門後有車和換門中車的差別
如果你那麼堅持自己的說法
那就用相同方式來解釋
「5門4羊1車,選一扇門又開啟一扇有羊的門,換門後中車機率是4/15」
你的腦袋真的比石頭還硬
我就和你說那是不同事件了,因為你把兩者混為一談我才同時提到
你根本沒搞清楚門後有車和換門中車的差別
如果你那麼堅持自己的說法
那就用相同方式來解釋
「5門4羊1車,選一扇門又開啟一扇有羊的門,換門後中車機率是4/15」
>>2185852
>>但是如果我拿出98顆黑球再讓你抽呢?你還會說抽出一顆球是白球的機率是1/100嗎?
這跟三門問題的情境根本不一樣= =
你已經從100顆球挑出98顆了 剩下就是二選一
三門問題是先選一顆再挑走 問你要不要換
這種在餃子店點包子的邏輯真是嘆為觀止
>>但是如果我拿出98顆黑球再讓你抽呢?你還會說抽出一顆球是白球的機率是1/100嗎?
這跟三門問題的情境根本不一樣= =
你已經從100顆球挑出98顆了 剩下就是二選一
三門問題是先選一顆再挑走 問你要不要換
這種在餃子店點包子的邏輯真是嘆為觀止
無題 無名 21/01/13(三)16:47:48 ID:gP2tldOw No.2185861
>>2185859
你是不是沒有點到展開文章....
你是不是沒有點到展開文章....
>>2185859
>你以為的情況是這樣
>一個袋子有1顆白球和99顆黑球
>現在你抽出一顆球是白球的機率是1/100
>但是如果我拿出98顆黑球再讓你抽呢?你還會說抽出一顆球是白球的機率是1/100嗎?
>而三門問題的情況是這樣
>一個袋子有1顆白球和99顆黑球
>現在讓你伸手進去選一顆球握住,我把其他98顆黑球取走
>然後問你,把手中的球換成另一顆,是白球的機率是多少
>因為你剛剛有99/100的機率握住黑球,只要剛剛握住的是黑>球,交換就會變成白球,所以才會有99/100的機率換得白球
抱歉,我這家餃子店就是有賣包子
把文章看完很難嗎?
>你以為的情況是這樣
>一個袋子有1顆白球和99顆黑球
>現在你抽出一顆球是白球的機率是1/100
>但是如果我拿出98顆黑球再讓你抽呢?你還會說抽出一顆球是白球的機率是1/100嗎?
>而三門問題的情況是這樣
>一個袋子有1顆白球和99顆黑球
>現在讓你伸手進去選一顆球握住,我把其他98顆黑球取走
>然後問你,把手中的球換成另一顆,是白球的機率是多少
>因為你剛剛有99/100的機率握住黑球,只要剛剛握住的是黑>球,交換就會變成白球,所以才會有99/100的機率換得白球
抱歉,我這家餃子店就是有賣包子
把文章看完很難嗎?
因為"打開一開始沒選的門"這個動作, 幫你開的一定是沒中獎的門
這不是一個隨機事件 <= 重點
所以"換門"和"選所有剩下的門"是等價的, 有3扇門就是2/3, 有100扇門就是99/100
違反直覺的就是這點
除非一開始你就選中了1/3或者1/100中的獎品那扇門
否則獎品一定在另一扇門中
兩扇門的機率根本完全不一樣
這不是一個隨機事件 <= 重點
所以"換門"和"選所有剩下的門"是等價的, 有3扇門就是2/3, 有100扇門就是99/100
違反直覺的就是這點
除非一開始你就選中了1/3或者1/100中的獎品那扇門
否則獎品一定在另一扇門中
兩扇門的機率根本完全不一樣
>>2185864
我沒有回過你,
也知道你看不懂, 沒有在回你
總之弄清楚一開始的那扇門的機率是1/N,
另一扇經過"打開所有沒中的門"之後是(N-1)/N,
還沒忘記中學機率的人就會明白了
我沒有回過你,
也知道你看不懂, 沒有在回你
總之弄清楚一開始的那扇門的機率是1/N,
另一扇經過"打開所有沒中的門"之後是(N-1)/N,
還沒忘記中學機率的人就會明白了
>>2185858
看在你這麼愚蠢的份上
我就浪費一點時間跟你解釋
>我知道有些人大概是看到回答過程出現1/2就急著出來喊錯
>但是如果把題目放大到5門4羊1車,選一扇門又開啟一扇有羊的門,就會了解並非全然不相關
>在這個問題中,和3扇門一樣,倘若你一開始選到中車的門,換門勢必會不中
>所以選到中車的門又換門的中車機是1/5*0=0
你都作出選擇了,機率怎麼還會是他媽的零
5門4羊1車, 那中獎機率就是1/5 不中機率是4/5
不要把全部的東西都歸類在中跟不中對你來說真的很難嗎?
>然而,如果你一開始選到不中的門,就算換門也不見得會中車
一開始沒中,所以抽到是4/5, 換門就變為剩下1/5
這不就是必定中獎?
有這麼難理解嗎?
>問題來了,假設你真的堅持門後有車的機率不會變,那可能就會進入死胡同
5門4羊1車,你告訴我門後有車的機率是要怎麼變?
從五抽一, 那就是五分之一, 你的胡同在哪, 講解一下好嗎
>你一開始選了不中的門,主持人又開啟一扇不中的門,剩下的3扇門中只有一扇是中的
>因此在「確定你已經選擇不中的門」這一條件下,換門中車的機率是1/3
你不要在他媽的亂改題目了, 你怎麼不乾脆說主持人太懶, 懶到不想開剩下的門算了
而且為什麼開啟的門一定會被移除, 門就他媽的好端端的立在那邊好嗎
>只是「換門中車的機率」並沒有設下第一次選擇是否中車的條件
>所以答案要同時計算
>一開始選到中車的門,換門後中車
>與
>一開始選到不中的門,換門後中車
>的機率
>即是(1/5*0)+(4/5*1/3)=4/15
你前面就搞錯了, 後面再怎麼精算都是浪費時間
>你的腦袋真的比石頭還硬
>我就和你說那是不同事件了,因為你把兩者混為一談我才同時提到
>你根本沒搞清楚門後有車和換門中車的差別
>如果你那麼堅持自己的說法
>那就用相同方式來解釋
門後只有羊或車, 那門後有車的機率就是1/2
你為什麼要他媽的這麼在意這1/2, 而去忽略門的數量?
>「5門4羊1車,選一扇門又開啟一扇有羊的門,換門後中車機率是4/15」
亂改題目帶來的垃圾, 如果真如你所說,你一開始選了羊門,主持人又開了ㄧ羊門
那你換門之後剩下3個門,機率就是1/3,
你不要再亂改題目了, 北妻
看在你這麼愚蠢的份上
我就浪費一點時間跟你解釋
>我知道有些人大概是看到回答過程出現1/2就急著出來喊錯
>但是如果把題目放大到5門4羊1車,選一扇門又開啟一扇有羊的門,就會了解並非全然不相關
>在這個問題中,和3扇門一樣,倘若你一開始選到中車的門,換門勢必會不中
>所以選到中車的門又換門的中車機是1/5*0=0
你都作出選擇了,機率怎麼還會是他媽的零
5門4羊1車, 那中獎機率就是1/5 不中機率是4/5
不要把全部的東西都歸類在中跟不中對你來說真的很難嗎?
>然而,如果你一開始選到不中的門,就算換門也不見得會中車
一開始沒中,所以抽到是4/5, 換門就變為剩下1/5
這不就是必定中獎?
有這麼難理解嗎?
>問題來了,假設你真的堅持門後有車的機率不會變,那可能就會進入死胡同
5門4羊1車,你告訴我門後有車的機率是要怎麼變?
從五抽一, 那就是五分之一, 你的胡同在哪, 講解一下好嗎
>你一開始選了不中的門,主持人又開啟一扇不中的門,剩下的3扇門中只有一扇是中的
>因此在「確定你已經選擇不中的門」這一條件下,換門中車的機率是1/3
你不要在他媽的亂改題目了, 你怎麼不乾脆說主持人太懶, 懶到不想開剩下的門算了
而且為什麼開啟的門一定會被移除, 門就他媽的好端端的立在那邊好嗎
>只是「換門中車的機率」並沒有設下第一次選擇是否中車的條件
>所以答案要同時計算
>一開始選到中車的門,換門後中車
>與
>一開始選到不中的門,換門後中車
>的機率
>即是(1/5*0)+(4/5*1/3)=4/15
你前面就搞錯了, 後面再怎麼精算都是浪費時間
>你的腦袋真的比石頭還硬
>我就和你說那是不同事件了,因為你把兩者混為一談我才同時提到
>你根本沒搞清楚門後有車和換門中車的差別
>如果你那麼堅持自己的說法
>那就用相同方式來解釋
門後只有羊或車, 那門後有車的機率就是1/2
你為什麼要他媽的這麼在意這1/2, 而去忽略門的數量?
>「5門4羊1車,選一扇門又開啟一扇有羊的門,換門後中車機率是4/15」
亂改題目帶來的垃圾, 如果真如你所說,你一開始選了羊門,主持人又開了ㄧ羊門
那你換門之後剩下3個門,機率就是1/3,
你不要再亂改題目了, 北妻
無題 無名 21/01/13(三)17:01:53 ID:sGXFZOE2 No.2185869
>>2185862
我想點個大麥克跟芝心披薩
你有沒有看到鴨肉店的下場? 不給我點就點你1星!
上面看不懂題目的都是歐皇0.000001%的單抽都一發入魂
你敢罵他們? 你不敢活啦!
但那隻鴿子為什麼那麼大? 你還沒回我啊!
我想點個大麥克跟芝心披薩
你有沒有看到鴨肉店的下場? 不給我點就點你1星!
上面看不懂題目的都是歐皇0.000001%的單抽都一發入魂
你敢罵他們? 你不敢活啦!
但那隻鴿子為什麼那麼大? 你還沒回我啊!
>>2185863
因為多數人沒察覺換門這個行為的意義
用球當例子就很容易懂
袋中有1顆白球99顆黑球
你伸手進去隨機握住1顆,然後我取出98顆黑球
現在只剩你握住的球和袋中另一顆球
也就是說如果你剛剛握住的是黑球,交換就會是白球,而你剛剛握住黑球的機率是____
此時,有個路人走來,他只知道你手中握住1顆顏色不明的球,袋中也有1顆顏色不明的球,他選中黑球的機率是____
多數人不了解交換的意義才以為自己是那個路人
因為多數人沒察覺換門這個行為的意義
用球當例子就很容易懂
袋中有1顆白球99顆黑球
你伸手進去隨機握住1顆,然後我取出98顆黑球
現在只剩你握住的球和袋中另一顆球
也就是說如果你剛剛握住的是黑球,交換就會是白球,而你剛剛握住黑球的機率是____
此時,有個路人走來,他只知道你手中握住1顆顏色不明的球,袋中也有1顆顏色不明的球,他選中黑球的機率是____
多數人不了解交換的意義才以為自己是那個路人
無題 無名 21/01/13(三)17:26:44 ID:ez3FSJAA No.2185879
還在吵
用真金白銀試一下不就好嗎
用真金白銀試一下不就好嗎
無題 無名 21/01/13(三)18:13:28 ID:SiQ3M9s2 No.2185890
無題 無名 21/01/13(三)18:50:05 ID:0LJRhCp2 No.2185894
靠么野太多篇
無題 無名 21/01/13(三)19:40:01 ID:/3CrFMQo No.2185909
duEcLL/w 不要再自創理論了啦
門後有車的機率一樣是1/3跟2/3啦
你都知道換跟不換得到車的機率不一樣,怎麼還會說出剩下兩個門都是50%這種白癡的話
門後有車的機率一樣是1/3跟2/3啦
你都知道換跟不換得到車的機率不一樣,怎麼還會說出剩下兩個門都是50%這種白癡的話
>>2185883
https://www.google.com/url?sa=t&source=web&rct=j&url=https://science.km.edu.tw/storage/media/332/58d6a4c27dfa4.pdf&ved=2ahUKEwjultLF75juAhWLxYsBHRwrC3MQFjAAegQIARAB&usg=AOvVaw3csThMeVHQ6pPLV9NkVKU6
你這pdf我看到了
你都說說了同樣開3扇門只剩2扇門,那根本沒變化
就是1/3跟2/3
因此你舉的「5門4羊1車,選一扇門又開啟一扇有羊的門,換門後中車機率是4/15」
本就不適用於3門時的情況
所以你的意思是你的1/2,是完全無關於3門的情況?
https://www.google.com/url?sa=t&source=web&rct=j&url=https://science.km.edu.tw/storage/media/332/58d6a4c27dfa4.pdf&ved=2ahUKEwjultLF75juAhWLxYsBHRwrC3MQFjAAegQIARAB&usg=AOvVaw3csThMeVHQ6pPLV9NkVKU6
你這pdf我看到了
你都說說了同樣開3扇門只剩2扇門,那根本沒變化
就是1/3跟2/3
因此你舉的「5門4羊1車,選一扇門又開啟一扇有羊的門,換門後中車機率是4/15」
本就不適用於3門時的情況
所以你的意思是你的1/2,是完全無關於3門的情況?
>>2185912
先去搞懂門後有車機率和換門中車機率的差異
兩者完全是不同事件
前者是1羊1車在2扇門後,這2扇門後是車羊的機率
後者是你選了一扇門,又換門中車的機率
你們就是錯在把前者拿去解釋後者,但是兩者根本不相關
先去搞懂門後有車機率和換門中車機率的差異
兩者完全是不同事件
前者是1羊1車在2扇門後,這2扇門後是車羊的機率
後者是你選了一扇門,又換門中車的機率
你們就是錯在把前者拿去解釋後者,但是兩者根本不相關
無題 無名 21/01/13(三)20:31:02 ID:ECQCVV.A No.2185925
>>2185924
習慣就好
習慣就好
無題 無名 21/01/13(三)20:37:01 ID:ZZOCU.kI No.2185928
說真的 不用跟他解釋了 這樣對大家都好
他已經完全陷入自己的神奇邏輯當中
兩扇門是50/50 但我換門又會變成1/3跟2/3 薛丁格的三門
要是他突然想通了 然後發現自己振振有詞的說了一堆邏輯錯亂的鬼話
換作是我會羞愧到想撞豆腐自殺......
也該慶幸是在K導匿名板啦 頂多自己在螢幕前羞憤
如果是在現實世界跟別人爭吵完才想通的話 應該會好一陣子不敢見到對方www
所以 你好我好大家好 就不用再試圖讓他理解了好嗎?
他已經完全陷入自己的神奇邏輯當中
兩扇門是50/50 但我換門又會變成1/3跟2/3 薛丁格的三門
要是他突然想通了 然後發現自己振振有詞的說了一堆邏輯錯亂的鬼話
換作是我會羞愧到想撞豆腐自殺......
也該慶幸是在K導匿名板啦 頂多自己在螢幕前羞憤
如果是在現實世界跟別人爭吵完才想通的話 應該會好一陣子不敢見到對方www
所以 你好我好大家好 就不用再試圖讓他理解了好嗎?
>>2185923
>開啟一扇有羊的門之後,就變成2選1,2扇門後有車的機率各是1/2
如果像你上面說,開啟一扇有羊的門之後,2扇門後有車的機率各是1/2
但你也說過,不換門就是1/3沒錯
所以如果我不換門,2扇門後有車的機率一樣各是1/2!?
說好的不換門就是1/3呢?
>開啟一扇有羊的門之後,就變成2選1,2扇門後有車的機率各是1/2
如果像你上面說,開啟一扇有羊的門之後,2扇門後有車的機率各是1/2
但你也說過,不換門就是1/3沒錯
所以如果我不換門,2扇門後有車的機率一樣各是1/2!?
說好的不換門就是1/3呢?
無題 無名 21/01/13(三)20:45:53 ID:ANyABgqc No.2185931
不要跟笨蛋爭論.jpg
這串看來,這句話真是至理名言
這串看來,這句話真是至理名言
無題 無名 21/01/13(三)20:50:23 ID:duEcLL/w No.2185932
>>2185919
那不是針對你
是另一個貼那篇pdf嗆我「5門4羊1車,選一扇門又開啟一扇有羊的門,換門後中車機率是4/15」錯誤,連小學生都不如的人
不過大概是發現自己看錯標題,幾分鐘後就刪了
另外一提,他上一個問的蠢問題是,這題目還剩3扇門怎麼知道要選哪扇
我說的沒變化是指題型
就像1白球2黑球抽中白球的機率,變成1白球4黑球抽中白球的機率
只要把數字換掉就能簡單得出答案,沒辦法鑑別是否真的理解
說1/2和這問題沒關係也沒錯
因為不必懂那件事也能得出這問題的正確答案,與其說是不適用,不如說根本用不到
那不是針對你
是另一個貼那篇pdf嗆我「5門4羊1車,選一扇門又開啟一扇有羊的門,換門後中車機率是4/15」錯誤,連小學生都不如的人
不過大概是發現自己看錯標題,幾分鐘後就刪了
另外一提,他上一個問的蠢問題是,這題目還剩3扇門怎麼知道要選哪扇
我說的沒變化是指題型
就像1白球2黑球抽中白球的機率,變成1白球4黑球抽中白球的機率
只要把數字換掉就能簡單得出答案,沒辦法鑑別是否真的理解
說1/2和這問題沒關係也沒錯
因為不必懂那件事也能得出這問題的正確答案,與其說是不適用,不如說根本用不到
>>2185924
這問題我說過很多次了
假設有個人從後半開始看,只看到一扇開啟的門有羊,另外兩扇門則是車和羊
請問他選中車的機率是多少?
這才是門後有車的機率
然而你是「換門後中車」的機率
你們的差異是你有先經過選門這機率,已經不是一個獨立事件
有沒有數學系島民出來解釋啊
每走一個就出來一個不懂我在說什麼的
現在在說的都已經和題目答案無關了
這問題我說過很多次了
假設有個人從後半開始看,只看到一扇開啟的門有羊,另外兩扇門則是車和羊
請問他選中車的機率是多少?
這才是門後有車的機率
然而你是「換門後中車」的機率
你們的差異是你有先經過選門這機率,已經不是一個獨立事件
有沒有數學系島民出來解釋啊
每走一個就出來一個不懂我在說什麼的
現在在說的都已經和題目答案無關了
無題 無名 21/01/13(三)21:09:13 ID:MtNdjYcg No.2185938
>>2185936
三門問題 從頭到尾都是在擁有所有題目資訊下如何作出最佳判斷的問題
就已經有一開始選擇與主持人開門的動作情報
你現在要跟人說
不要管前面作了甚麼事情 你失憶了
現在就兩扇門在你面前 他們的機率是多少?
是的 對那位沒有足夠情報的人來說 他只能作出1/2跟1/2的判斷
但對於從頭到尾都看在眼裡的人來說 那就是1/3跟2/3
你這要求就跟把包子的內餡扔掉然後說"這是饅頭對吧?"
是的 基本上沒錯 但所有人都在跟你討論這包子好不好吃 你在那邊說他是饅頭?
然後在那邊喊說你們這些白癡都不知道包子的內餡拿掉就是饅頭了!!
真的只能說 你到底在供三小...
三門問題 從頭到尾都是在擁有所有題目資訊下如何作出最佳判斷的問題
就已經有一開始選擇與主持人開門的動作情報
你現在要跟人說
不要管前面作了甚麼事情 你失憶了
現在就兩扇門在你面前 他們的機率是多少?
是的 對那位沒有足夠情報的人來說 他只能作出1/2跟1/2的判斷
但對於從頭到尾都看在眼裡的人來說 那就是1/3跟2/3
你這要求就跟把包子的內餡扔掉然後說"這是饅頭對吧?"
是的 基本上沒錯 但所有人都在跟你討論這包子好不好吃 你在那邊說他是饅頭?
然後在那邊喊說你們這些白癡都不知道包子的內餡拿掉就是饅頭了!!
真的只能說 你到底在供三小...
>>2185929
注意描述的對象
「門後面是車」的機率和「換門後中車」的機率不同也不相關
因為場上只剩兩扇門,你開啟其中一扇門,門後是車的機率是1/2
然而,這不是三門問題要的
三門問題的情況有幾種
第一次中車,換門不中
第一次中車,換門中車
第一次不中,換門中車
第一次不中,換門不中
因為2、4項機率是0,就不去探討
第1項的機率是1/3(第一次中車)×1(換門不中)=1/3
第3項的機率是2/3(第一次不中)×1(換門中車)=2/3
這就是不換門中車機率是1/3,換門中車機率是2/3的原因
並不是主持人開門之後門後有車機率是1/3,1/3是你不換門中車的機率
注意描述的對象
「門後面是車」的機率和「換門後中車」的機率不同也不相關
因為場上只剩兩扇門,你開啟其中一扇門,門後是車的機率是1/2
然而,這不是三門問題要的
三門問題的情況有幾種
第一次中車,換門不中
第一次中車,換門中車
第一次不中,換門中車
第一次不中,換門不中
因為2、4項機率是0,就不去探討
第1項的機率是1/3(第一次中車)×1(換門不中)=1/3
第3項的機率是2/3(第一次不中)×1(換門中車)=2/3
這就是不換門中車機率是1/3,換門中車機率是2/3的原因
並不是主持人開門之後門後有車機率是1/3,1/3是你不換門中車的機率
文組低能真的很好騙耶
上面早就說過了
換或不換機率是一樣的
那些機率改變的全都被帶風向把問題想複雜了
你要怎知道你換門前選的有沒有獎勵勒
感覺都預設換門前選到沒獎勵的
然後被帶風向給騙到認為換過就比較高
不管怎麼換原始機率是不變的
因為你還沒把門打開看過門後有什麼
之後開了一個空的門來誘騙你換門
但實際機率是還是一樣的
不會因此變多
上面早就說過了
換或不換機率是一樣的
那些機率改變的全都被帶風向把問題想複雜了
你要怎知道你換門前選的有沒有獎勵勒
感覺都預設換門前選到沒獎勵的
然後被帶風向給騙到認為換過就比較高
不管怎麼換原始機率是不變的
因為你還沒把門打開看過門後有什麼
之後開了一個空的門來誘騙你換門
但實際機率是還是一樣的
不會因此變多
無題 無名 21/01/13(三)21:25:34 ID:duEcLL/w No.2185949
>>2185944
>就是有人不懂,而且還不少
>有些人就是不瞭解,1/3不是主持人開門之後門後有車的機率,>1/3是你不換門中車的機率
我快笑死了,不懂的就是說你啊
中車=門後有車
中車的機率=門後有車的機率
為什麼你會覺得不一樣
>1/3是你不換門中車的機率
所以不換門,門後有車的機率就是1/3阿,不然中個屁車
>就是有人不懂,而且還不少
>有些人就是不瞭解,1/3不是主持人開門之後門後有車的機率,>1/3是你不換門中車的機率
我快笑死了,不懂的就是說你啊
中車=門後有車
中車的機率=門後有車的機率
為什麼你會覺得不一樣
>1/3是你不換門中車的機率
所以不換門,門後有車的機率就是1/3阿,不然中個屁車
無題 無名 21/01/13(三)21:28:31 ID:duEcLL/w No.2185952
無題 無名 21/01/13(三)21:30:10 ID:ZZOCU.kI No.2185953
>>2185946
對我這個想盤子的文組廢物要來送聰明的大大錢了
我可以過去找你 或者你過來找我 我出車馬費
三門問題我們來實際操作 我當主持人
把門跟獎品改成乒乓球
也就是三個杯子+三顆乒乓球 其中一顆顏色不同
你主張換跟不換機率都是50%
因此我要求你一開始選完後
我開一個杯子給你看 你必須選擇不換杯子
如果你選中了 我給你6000元
如果你沒選中 你給我4000元
照你的主張 平均每玩2次我們會各贏一次
我要給你6000 你要給我4000 一來一往 我要給你2000
你平均每場可以賺1000元
為了避免過低樣本數的運氣誤差 我們玩個100次
這樣你可以賺1000*100=10萬元
好不好好不好好不好好不好好不好
我好想要送你錢拜託拜託拜託拜託拜託
對我這個想盤子的文組廢物要來送聰明的大大錢了
我可以過去找你 或者你過來找我 我出車馬費
三門問題我們來實際操作 我當主持人
把門跟獎品改成乒乓球
也就是三個杯子+三顆乒乓球 其中一顆顏色不同
你主張換跟不換機率都是50%
因此我要求你一開始選完後
我開一個杯子給你看 你必須選擇不換杯子
如果你選中了 我給你6000元
如果你沒選中 你給我4000元
照你的主張 平均每玩2次我們會各贏一次
我要給你6000 你要給我4000 一來一往 我要給你2000
你平均每場可以賺1000元
為了避免過低樣本數的運氣誤差 我們玩個100次
這樣你可以賺1000*100=10萬元
好不好好不好好不好好不好好不好
我好想要送你錢拜託拜託拜託拜託拜託
無題 無名 21/01/13(三)21:31:34 ID:MtNdjYcg No.2185954
>>2185946
>然後被帶風向給騙到認為換過就比較高
https://www.google.com/url?sa=t&source=web&rct=j&url=https://science.km.edu.tw/storage/media/332/58d6a4c27dfa4.pdf&ved=2ahUKEwjultLF75juAhWLxYsBHRwrC3MQFjAAegQIARAB&usg=AOvVaw3csThMeVHQ6pPLV9NkVKU6
請看看,這是小學生做的,你讀一讀裡面有沒有驗證,換過中車率是不是比較高
>然後被帶風向給騙到認為換過就比較高
https://www.google.com/url?sa=t&source=web&rct=j&url=https://science.km.edu.tw/storage/media/332/58d6a4c27dfa4.pdf&ved=2ahUKEwjultLF75juAhWLxYsBHRwrC3MQFjAAegQIARAB&usg=AOvVaw3csThMeVHQ6pPLV9NkVKU6
請看看,這是小學生做的,你讀一讀裡面有沒有驗證,換過中車率是不是比較高
同樣是三門遊戲,這次來了三個參與者甲、乙、丙,他們一人選擇了一扇門。這時候主持人打開了丙的門,告訴他,你的是羊,抱著走吧。然後問甲、乙是不是要換門,甲和乙都想得到車,都是知道三門問題答案的理性成年人,自然也想到換一個門有2/3的機會得到車,於是甲換到乙門,乙換到甲門。剛站好,同時發覺是不是哪裡搞錯了,於是面面相覷,有瞬間理性人變二師兄的感覺。
>>2185955
不,從頭到尾都是你在跳針
這邊是討論三門問題
你如果要忽略選門和主持人開門,搞個不一樣的題目請另外開串去討論
在原題目的選門和開門的前提下
「(不)換門後中車」的機率和「門後有車」的機率就是一樣
連中車就等於門後有車都理解不了
中文有問題的人說別人有問題w
不,從頭到尾都是你在跳針
這邊是討論三門問題
你如果要忽略選門和主持人開門,搞個不一樣的題目請另外開串去討論
在原題目的選門和開門的前提下
「(不)換門後中車」的機率和「門後有車」的機率就是一樣
連中車就等於門後有車都理解不了
中文有問題的人說別人有問題w
無題 無名 21/01/13(三)22:03:12 ID:In17r2h. No.2185962
>>2185956
甲乙丙三人各選一扇門且不重複 則每人獲得車的機率為1/3
主持人打開丙的門 門後是羊
則代表甲或乙其中一人選到了後方有車的那扇門
更換後獲得車的機率為2/3 選中車的換變成羊 選中羊的換變成車
模型成立
如果你要甲乙兩人獲得車的機率為1/2
那必須"揭開丙的羊門後 再讓甲乙去選擇要哪扇門"
甲乙丙三人各選一扇門且不重複 則每人獲得車的機率為1/3
主持人打開丙的門 門後是羊
則代表甲或乙其中一人選到了後方有車的那扇門
更換後獲得車的機率為2/3 選中車的換變成羊 選中羊的換變成車
模型成立
如果你要甲乙兩人獲得車的機率為1/2
那必須"揭開丙的羊門後 再讓甲乙去選擇要哪扇門"
不懂你們還在爭執什麼,這麼長下來一串明顯>>duEcLL/w 就是自以為聰明硬要拆題的猴子,跟其他腦細胞死到硬要抱著1/2的猴子根本就沒差
猴子能了解人類的知識嗎?
數學問題我們人類懂了不就好了?
猴子能了解人類的知識嗎?
數學問題我們人類懂了不就好了?
無題 無名 21/01/13(三)22:23:58 ID:EQ/HQ8K6 No.2185970
無本文
有回應 412 篇被省略。[展開]
????????????????????
有回應 412 篇被省略。[展開]
????????????????????
無題 無名 21/01/13(三)22:30:01 ID:KcJSpedI No.2185971
>>2185956
自以為聰明再來一個,對甲乙來說一樣是換門更有利
因為你無從得知自己一開始選到的到底是車還是羊,所以換門條件仍然成立
搞清楚三門問題的的解答並不是讓你包中車而是讓機率從1/3上升到2/3,換門是"有利"而不是"保證"
死守著原本的門也只是讓有利條件白白飛走而已
說白了死抓著同樣機率論述的猴子們不是不喜歡承認自己笨的笨蛋,就是連賭博本身就是數學遊戲都不懂而盲目相信自己運氣的孬種
跟這些垃圾講理論是沒有用的,不然敢像上面一堆人說的來對賭啊?
自以為聰明再來一個,對甲乙來說一樣是換門更有利
因為你無從得知自己一開始選到的到底是車還是羊,所以換門條件仍然成立
搞清楚三門問題的的解答並不是讓你包中車而是讓機率從1/3上升到2/3,換門是"有利"而不是"保證"
死守著原本的門也只是讓有利條件白白飛走而已
說白了死抓著同樣機率論述的猴子們不是不喜歡承認自己笨的笨蛋,就是連賭博本身就是數學遊戲都不懂而盲目相信自己運氣的孬種
跟這些垃圾講理論是沒有用的,不然敢像上面一堆人說的來對賭啊?
>>2185965
別再拿圖片自婊了
隨便舉個不相關的例子就很好懂
有AB兩扇門,你知道其中一扇門後是車另一扇是羊
A門有1/3機率能一次打開,B門有1/5機率能一次打開,要一次打開門車才是你的
請問
1.AB門門後有車的機率各是多少?
2.你中車子的機率是多少?
別哭我又拿不相關的例子
這個例子只是要說明在複數條件下中車的機率和門後有車的機率他x的不一樣
而「(不)換門後中車」的機率就他x的不是獨立事件
別再拿圖片自婊了
隨便舉個不相關的例子就很好懂
有AB兩扇門,你知道其中一扇門後是車另一扇是羊
A門有1/3機率能一次打開,B門有1/5機率能一次打開,要一次打開門車才是你的
請問
1.AB門門後有車的機率各是多少?
2.你中車子的機率是多少?
別哭我又拿不相關的例子
這個例子只是要說明在複數條件下中車的機率和門後有車的機率他x的不一樣
而「(不)換門後中車」的機率就他x的不是獨立事件
無題 無名 21/01/13(三)22:38:28 ID:KcJSpedI No.2185977
>>2185972
你講一堆屁話跟三門問題有相關嗎?智障
你以為為什麼是三門問題被流傳下來廣泛討論而不是五門?八門?十門?一百門?還是上面一堆為了解釋給你聽想出來的亂七八糟變體
還在刁三小"中車的機率和門後有車的機率"就表明了你一開始就沒在討論三門問題或是根本不了解這個問題的原理
我就大發慈悲告訴你答案好了,不換門中車的機率是1/3,門後有車的機率也是一樣是1/3啦!
你以為你知道其中一扇門的答案後門就不存在了是不是?這就是你這猴子跟我們人類的差別啦,三門問題最後會有三組不同的答案就讓分母永遠不可能會是2啦!
你講一堆屁話跟三門問題有相關嗎?智障
你以為為什麼是三門問題被流傳下來廣泛討論而不是五門?八門?十門?一百門?還是上面一堆為了解釋給你聽想出來的亂七八糟變體
還在刁三小"中車的機率和門後有車的機率"就表明了你一開始就沒在討論三門問題或是根本不了解這個問題的原理
我就大發慈悲告訴你答案好了,不換門中車的機率是1/3,門後有車的機率也是一樣是1/3啦!
你以為你知道其中一扇門的答案後門就不存在了是不是?這就是你這猴子跟我們人類的差別啦,三門問題最後會有三組不同的答案就讓分母永遠不可能會是2啦!
無題 無名 21/01/13(三)22:48:22 ID:ECQCVV.A No.2185982
>>2185980
放棄吧
放棄吧
>>2185980
3扇門後必定有1車2羊
開啟一扇門有羊的門之後,剩餘2扇門後必定有1車1羊
然後你說這兩扇門門後有車的機率都是1/3
太神奇了,我打開剩下這兩扇門竟然只有2/3機率得到車
如果你定義的人類是如此
那猴子還比較聰明
3扇門後必定有1車2羊
開啟一扇門有羊的門之後,剩餘2扇門後必定有1車1羊
然後你說這兩扇門門後有車的機率都是1/3
太神奇了,我打開剩下這兩扇門竟然只有2/3機率得到車
如果你定義的人類是如此
那猴子還比較聰明
無題 無名 21/01/13(三)22:52:01 ID:ECQCVV.A No.2185987
>>2185981
所以為什麼三門問題到了你這裡就會變成你選的門變成開啟狀態了
一開始不是盲選三選一嗎
三個門 每扇門只有一扇有獎品
所以中獎機率是三分之一
你不要在拿門後是車還是羊的智障二分之一理論來亂了好嗎
還什麼門後有車的機率是零
門後面不是羊就是車 哪來的零
所以為什麼三門問題到了你這裡就會變成你選的門變成開啟狀態了
一開始不是盲選三選一嗎
三個門 每扇門只有一扇有獎品
所以中獎機率是三分之一
你不要在拿門後是車還是羊的智障二分之一理論來亂了好嗎
還什麼門後有車的機率是零
門後面不是羊就是車 哪來的零
>>2185981
>>你該不會要說有羊那扇被開啟的門門後有車的機率是1/3吧
正確答案,會W這句話表示你還是不懂數學
開門後三門問題的答案一樣會有三種:不換(一種贏兩種輸)換(兩種贏一種輸),如果解題中間就刪去一扇門了那最後的解答就不能回推到原點,又不是說門開了存在之力就會被消去殺小的
我懂你的問題了,你一定沒聽過三囚問題對不對?猴子
>>你該不會要說有羊那扇被開啟的門門後有車的機率是1/3吧
正確答案,會W這句話表示你還是不懂數學
開門後三門問題的答案一樣會有三種:不換(一種贏兩種輸)換(兩種贏一種輸),如果解題中間就刪去一扇門了那最後的解答就不能回推到原點,又不是說門開了存在之力就會被消去殺小的
我懂你的問題了,你一定沒聽過三囚問題對不對?猴子
無題 無名 21/01/13(三)22:53:01 ID:ECQCVV.A No.2185989
>>2185986
>>打開剩下這兩扇門竟然只有2/3機率得到車
2/3是換門中獎的機率而不是打開兩扇門,全部開門當然是100%中獎阿
所以不換門打開後是車有1/3機率,換門打開有2/3機率,全開就是100%全中(或是你要硬刁就是3/3機率)
那你的1/2到底是從哪裡的肛門拉出來的?
猴子
>>打開剩下這兩扇門竟然只有2/3機率得到車
2/3是換門中獎的機率而不是打開兩扇門,全部開門當然是100%中獎阿
所以不換門打開後是車有1/3機率,換門打開有2/3機率,全開就是100%全中(或是你要硬刁就是3/3機率)
那你的1/2到底是從哪裡的肛門拉出來的?
猴子
無題 無名 21/01/13(三)22:58:21 ID:UX86S6AE No.2185993
文組腦子都是這樣啦
你問文組樂透的機率多少 他們只會回答1/2 不就中或不中而已?
你問文組樂透的機率多少 他們只會回答1/2 不就中或不中而已?
無題 無名 21/01/13(三)22:58:46 ID:KcJSpedI No.2185994
>>2185995
duEcLL/w終於承認自己是猴子了!大家可以回家啦!
duEcLL/w終於承認自己是猴子了!大家可以回家啦!
無題 無名 21/01/13(三)23:05:44 ID:0tlk3H7. No.2185997
>>2185990
自稱「人類」卻搞不懂我說什麼w
你自己說開門之後門後有車的機率一樣是1/3
那照理說這兩扇門門後有車的機率加起來要是1,因為被開啟的那扇門門後是車的機率是0
結果你這兩扇門門後有車的機率加起來只有2/3
兩扇門都開還不見得中車,神奇!
自稱「人類」的奸詐不為過w
自稱「人類」卻搞不懂我說什麼w
你自己說開門之後門後有車的機率一樣是1/3
那照理說這兩扇門門後有車的機率加起來要是1,因為被開啟的那扇門門後是車的機率是0
結果你這兩扇門門後有車的機率加起來只有2/3
兩扇門都開還不見得中車,神奇!
自稱「人類」的奸詐不為過w
無題 無名 21/01/13(三)23:38:48 ID:bVRKeGdU No.2186006
duEcLL/w邏輯就是
不換門,這扇門中車的機率是1/3,但是這扇門後面有車的機率是1/2
換了門,這扇門中車的機率是2/3,但是這扇門後面有車的機率是1/2
大家快來看智障
不換門,這扇門中車的機率是1/3,但是這扇門後面有車的機率是1/2
換了門,這扇門中車的機率是2/3,但是這扇門後面有車的機率是1/2
大家快來看智障
無題 無名 21/01/13(三)23:40:16 ID:KcJSpedI No.2186007
無題 無名 21/01/13(三)23:40:54 ID:c67hAGWE No.2186008
>>2186004
主持人:這次獎品不是奇美拉
主持人:這次獎品不是奇美拉
>>2186004
機率確實不會變啊 因為你一開始選定的門是在"三門未知"情況下的選擇
只有"先開一扇後方有羊的門再給你選"才會是1/2的選擇
假設今有ABC三門 只知其後兩羊一車
不知車在哪扇門後 所以ABC三門後方有車的機率各是1/3
你選擇了A門 將A門設為α組 α組後方有車的機率為1/3
剩下的BC兩門設為β組 β組後方有車的機率為B門1/3+C門1/3=2/3
主持人揭開B門 是羊
α組的機率仍為1/3 因為"這是你在揭開B門前的選擇"
β組的機率仍為2/3 因為"B門後方沒車 因此C門是車的機率增加了"
機率確實不會變啊 因為你一開始選定的門是在"三門未知"情況下的選擇
只有"先開一扇後方有羊的門再給你選"才會是1/2的選擇
假設今有ABC三門 只知其後兩羊一車
不知車在哪扇門後 所以ABC三門後方有車的機率各是1/3
你選擇了A門 將A門設為α組 α組後方有車的機率為1/3
剩下的BC兩門設為β組 β組後方有車的機率為B門1/3+C門1/3=2/3
主持人揭開B門 是羊
α組的機率仍為1/3 因為"這是你在揭開B門前的選擇"
β組的機率仍為2/3 因為"B門後方沒車 因此C門是車的機率增加了"
無題 無名 21/01/13(三)23:51:09 ID:KcJSpedI No.2186011
>>2186009
他的下一句會是:"錯,因為開啟的一扇門已經百分之百確定是羊,所以剩下兩扇門中一定有一扇是車,故機率是1/2.我就說了一開始選門跟開啟門後是兩個分開的事件!"
他的下一句會是:"錯,因為開啟的一扇門已經百分之百確定是羊,所以剩下兩扇門中一定有一扇是車,故機率是1/2.我就說了一開始選門跟開啟門後是兩個分開的事件!"
"隨機"(例如丟硬幣決定)從剩下兩扇門中選一扇是1/2
不換是1/3
換是2/3
換跟不換都不是"隨機選"
這樣解釋應該夠清楚吧
不換是1/3
換是2/3
換跟不換都不是"隨機選"
這樣解釋應該夠清楚吧
無題 無名 21/01/14(四)00:13:44 ID:PxEKtYmk No.2186014
>>2186012
NONONO
真隨機開門的話 在一開始沒選到門的狀況下 可能會開出有車的門
但打開有車的門當下就違反遊戲規則了
如果要堅持隨機又要在一定程度維護規則方法 就只能隨機選出後不打開門就直接撤掉
這樣A門有車的機率 1/3 B門有車的機率1/3 兩扇門都沒有車的機率1/3(因為被撤走了)
NONONO
真隨機開門的話 在一開始沒選到門的狀況下 可能會開出有車的門
但打開有車的門當下就違反遊戲規則了
如果要堅持隨機又要在一定程度維護規則方法 就只能隨機選出後不打開門就直接撤掉
這樣A門有車的機率 1/3 B門有車的機率1/3 兩扇門都沒有車的機率1/3(因為被撤走了)
無題 無名 21/01/14(四)00:21:48 ID:9ama1r52 No.2186019
數學真的難 不會就是不會
無題 無名 21/01/14(四)00:27:20 ID:AMZ.ejuM No.2186022
今天,你身處支那,想找一個還沒被主席調教成肉便器的自由鬥士,你要在14億人口中找那一人,在沒有任何頭緒的狀態下,你找了你身旁的一位看起來和藹可親的大嬸
這時,你收到了一通加密電話,這是一個來自自由國家的人,並表示這名自由鬥士很可能是(A),但玩家自己找的(B)也是有可能是正解
此刻,數學小天才立刻表示:我選到正確的人是1/2,選那個人也是1/2,就只有兩個人讓我選,你排除其他14億-2人的動作毫無意義,這沒什麼差別吧
這時,你收到了一通加密電話,這是一個來自自由國家的人,並表示這名自由鬥士很可能是(A),但玩家自己找的(B)也是有可能是正解
此刻,數學小天才立刻表示:我選到正確的人是1/2,選那個人也是1/2,就只有兩個人讓我選,你排除其他14億-2人的動作毫無意義,這沒什麼差別吧
這種題目最大問題是
到底可以換幾次門阿
⊂彡☆))д`)< 可以選擇打開主持人的後門嗎
到底可以換幾次門阿
⊂彡☆))д`)< 可以選擇打開主持人的後門嗎
無題 無名 21/01/14(四)00:56:59 ID:EkA8ebxA No.2186028
>>2186025
假設C門後是車
不換門的情況下
1.選擇A門 沒有車
2.選擇B門 沒有車
3.選擇C門 有車
所以不換門機率為1/3
換門的情況下
1.選擇A門 主持人會開啟B門 所以就會換成C門 有車
2.選擇B門 主持人會開啟A門 所以就會換成C門 有車
3.選擇C門 主持人開啟A/B門 所以會換成A/B門 都沒有車
所以換門機率為2/3
假設C門後是車
不換門的情況下
1.選擇A門 沒有車
2.選擇B門 沒有車
3.選擇C門 有車
所以不換門機率為1/3
換門的情況下
1.選擇A門 主持人會開啟B門 所以就會換成C門 有車
2.選擇B門 主持人會開啟A門 所以就會換成C門 有車
3.選擇C門 主持人開啟A/B門 所以會換成A/B門 都沒有車
所以換門機率為2/3
無題 無名 21/01/14(四)01:16:14 ID:bMg2ZBN. No.2186032
無題 無名 21/01/14(四)01:23:38 ID:6NQf2o3A No.2186035
這串 很明顯的凸顯了 雖然搞懂的人很多 但是不是每個人都適合當老師
我一開始也是不懂 直到我把整個問題倒過來念 就瞬間理解了
知道為什麼的人 不知道不理解的人 不理解的點在哪裡
不理解的人 不理解知道的人 知道了些什麼問題
只要解釋沒有觸碰到 不理解的人所不理解的問題點 再多的解釋跟算式 舉例都沒辦法解開那個點
但是只要 那個點對了 不用解釋也不用算式 就能夠瞬間理解了
還在努力解釋為什麼不是二分之一的人 加油
我一開始也是不懂 直到我把整個問題倒過來念 就瞬間理解了
知道為什麼的人 不知道不理解的人 不理解的點在哪裡
不理解的人 不理解知道的人 知道了些什麼問題
只要解釋沒有觸碰到 不理解的人所不理解的問題點 再多的解釋跟算式 舉例都沒辦法解開那個點
但是只要 那個點對了 不用解釋也不用算式 就能夠瞬間理解了
還在努力解釋為什麼不是二分之一的人 加油
其實是先後順序的差別
如果主持人先讓你看山羊再選
另外兩道門一定是一隻羊一台車
所以機率可以是1/2
但是你先選了主持人才讓你看山羊
那麼你一開始選擇的機率就是1/3了
如果主持人先讓你看山羊再選
另外兩道門一定是一隻羊一台車
所以機率可以是1/2
但是你先選了主持人才讓你看山羊
那麼你一開始選擇的機率就是1/3了
無題 無名 21/01/14(四)01:45:22 ID:6NQf2o3A No.2186042
>>2184867
預言家
預言家
無題 無名 21/01/14(四)01:45:28 ID:PxEKtYmk No.2186044
>>2185812
具體的機率模型牽涉到的變數太多 要弄具體的機率模型太複雜
但因為開串是三門問題所以我假定
1.你的消去使用前可以如同三門問題一樣 先選擇一個讓他不在排除法的選擇樣本範圍
2.有兩個以上的可能正確答案(只有一個的話就直接選了刪屁刪)
3.一般的選擇題應該是4選1
4.刪除先假定只刪除一個
5.消去後一定會保留正確答案
那麼 具體的機率模型沒法列出來 但我可以告訴你一個絕對適用的通則
"先選你覺得最不可能是答案的選項再使用消去"
為什麼這樣做的理由也很簡單 因為你心目中有復數可能的答案
希望利用消去把你覺得可能的選擇數量壓低後重新評估選擇
那麼那個"最不可能的答案"若是被消去的話 實質上不會對你的決策流程產生任何幫助
但把最不可能的答案先保留祝 再刪除其他選項的話 某種意義上就等同於排除了兩個選項
當然這個前題是你對題目有基本的認知跟評估 如果題目完全看不懂 四個選項感覺機率都一樣的話
那你怎麼選怎麼操作 實際上都沒有多大意義
啊 可是最後還是要換選項機率會稍微高一點就是了
具體的機率模型牽涉到的變數太多 要弄具體的機率模型太複雜
但因為開串是三門問題所以我假定
1.你的消去使用前可以如同三門問題一樣 先選擇一個讓他不在排除法的選擇樣本範圍
2.有兩個以上的可能正確答案(只有一個的話就直接選了刪屁刪)
3.一般的選擇題應該是4選1
4.刪除先假定只刪除一個
5.消去後一定會保留正確答案
那麼 具體的機率模型沒法列出來 但我可以告訴你一個絕對適用的通則
"先選你覺得最不可能是答案的選項再使用消去"
為什麼這樣做的理由也很簡單 因為你心目中有復數可能的答案
希望利用消去把你覺得可能的選擇數量壓低後重新評估選擇
那麼那個"最不可能的答案"若是被消去的話 實質上不會對你的決策流程產生任何幫助
但把最不可能的答案先保留祝 再刪除其他選項的話 某種意義上就等同於排除了兩個選項
當然這個前題是你對題目有基本的認知跟評估 如果題目完全看不懂 四個選項感覺機率都一樣的話
那你怎麼選怎麼操作 實際上都沒有多大意義
啊 可是最後還是要換選項機率會稍微高一點就是了
>>2186041
難不成主持人給你第二次選擇機會的同時還對你施放洗腦嗎?
不然怎麼會忘記了之前的所有可供判斷機率的資料得到了神奇的1/2?
主持人給的第二次選擇機會 是你可以經由自己的判斷仔細思考選擇的第二次機會
不是叫你閉著眼睛讓你抽一次啊......
難不成主持人給你第二次選擇機會的同時還對你施放洗腦嗎?
不然怎麼會忘記了之前的所有可供判斷機率的資料得到了神奇的1/2?
主持人給的第二次選擇機會 是你可以經由自己的判斷仔細思考選擇的第二次機會
不是叫你閉著眼睛讓你抽一次啊......
無題 無名 21/01/14(四)01:59:06 ID:6NQf2o3A No.2186050
我用我理解的方式 說明一下 希望能讓還沒理解的人也知道
雖然這個理解方法可能是錯的但是 也許能讓沒理解的人跳脫 二分之一的問題點
三扇門 一開始就選中 車的機率是 三分之一
中間打開了一扇 確定沒有中獎 但此時請不要直接將這扇門刪去
他還是存在 主持人問要不要換門 這個時候 如果選擇不換 那麼你中獎的機率就還是一開始的三選一的三分之一
不管有沒有門被打開 不換門就是三分之一
但是如果你選擇換了 就會變成 連同已經開了的門也一起選了
換門等於是打開兩扇門 一扇是已經知道結果的門一扇是還沒打開的門
一次選了兩道門 這樣 就等於吃掉了原本三選一 三分之二的機率部分
當然一次選了兩扇門的話 只要有一扇中獎就行
理解這點之後就 再看看上面說的那些舉例跟公式就能完全理解的
雖然這個理解方法可能是錯的但是 也許能讓沒理解的人跳脫 二分之一的問題點
三扇門 一開始就選中 車的機率是 三分之一
中間打開了一扇 確定沒有中獎 但此時請不要直接將這扇門刪去
他還是存在 主持人問要不要換門 這個時候 如果選擇不換 那麼你中獎的機率就還是一開始的三選一的三分之一
不管有沒有門被打開 不換門就是三分之一
但是如果你選擇換了 就會變成 連同已經開了的門也一起選了
換門等於是打開兩扇門 一扇是已經知道結果的門一扇是還沒打開的門
一次選了兩道門 這樣 就等於吃掉了原本三選一 三分之二的機率部分
當然一次選了兩扇門的話 只要有一扇中獎就行
理解這點之後就 再看看上面說的那些舉例跟公式就能完全理解的
無題 無名 21/01/14(四)02:02:17 ID:iexqb80U No.2186052
主持人開掉一個
你確定"不需要"的獎品了
你確定"不需要"的獎品了
>>2186047
一開始3選1的隨機選取
選中車的機率僅有1/3
反過來說
車子在另外兩扇門其中一的機率有2/3
這時候你要認知到一件很重要的事情
排除掉節目單位作弊之類的人為因素(數學題不討論這種東西)
你一開始選擇的門後面有沒有車 你雖然無法知道
但在上帝視角(或者你可以想像成電視台的某位幕後工作人員)
你的門後面有車就是有車 沒車就是沒車
不管主持人是幫你開了另外一扇門 又或者是在那兩扇門之外又多加了一百扇門
你一開始選擇的門他後面到底有沒有車這個問題
在你選擇的當下就已經被決定了(只是沒有被你自己給觀察確認)
而那個機率是多少呢?
一開始3選1的隨機選取
選中車的機率僅有1/3
反過來說
車子在另外兩扇門其中一的機率有2/3
這時候你要認知到一件很重要的事情
排除掉節目單位作弊之類的人為因素(數學題不討論這種東西)
你一開始選擇的門後面有沒有車 你雖然無法知道
但在上帝視角(或者你可以想像成電視台的某位幕後工作人員)
你的門後面有車就是有車 沒車就是沒車
不管主持人是幫你開了另外一扇門 又或者是在那兩扇門之外又多加了一百扇門
你一開始選擇的門他後面到底有沒有車這個問題
在你選擇的當下就已經被決定了(只是沒有被你自己給觀察確認)
而那個機率是多少呢?
無題 無名 21/01/14(四)02:07:36 ID:kL3Ztoow No.2186054
無題 無名 21/01/14(四)02:14:27 ID:vFXlNnHc No.2186056
覺得是1/2的可以看看>>2185795嗎
我寫得好辛苦的(?
我寫得好辛苦的(?
無題 無名 21/01/14(四)02:15:59 ID:PxEKtYmk No.2186058
>>2186055
好吧 先不要管機率 你願意的話就讓我們來實際操作一遍
沒有辦法接受理論我們就來實操一次
https://www.ifreesite.com/textencrypt/
這是一個線上的加解密網站
我用他進行了一個30個數字的加密字串
內容是1~3隨機選擇
類似這樣
11111 22222
33333 11111
22222 33333
當然上面的123都是隨機打亂沒有這麼整齊排序的
為了確保我沒有作弊我這邊先放上加密後的字串(有設密碼你不能直接解密)
U2FsdGVkX18dnUHgcYIbXO5IU6bB862j28L8CHBb52BeHFths85+WyOQixnF1NsU
gSdLGilh2w/yMzqB16dd4g==
在你進行了30次的數字選擇後
我會幫你排除一個數字(絕對不會排除到上面已記錄的數字)
你可以任意選擇是否要更換(我建議為了方便是統一全部換獲全不不換 但不強迫)
你選擇完之後 我再公開密碼大家一起對答案 可以嗎?
簡單來說就是你一人分飾30腳同時平行進行一次三門問題實際演練
好吧 先不要管機率 你願意的話就讓我們來實際操作一遍
沒有辦法接受理論我們就來實操一次
https://www.ifreesite.com/textencrypt/
這是一個線上的加解密網站
我用他進行了一個30個數字的加密字串
內容是1~3隨機選擇
類似這樣
11111 22222
33333 11111
22222 33333
當然上面的123都是隨機打亂沒有這麼整齊排序的
為了確保我沒有作弊我這邊先放上加密後的字串(有設密碼你不能直接解密)
U2FsdGVkX18dnUHgcYIbXO5IU6bB862j28L8CHBb52BeHFths85+WyOQixnF1NsU
gSdLGilh2w/yMzqB16dd4g==
在你進行了30次的數字選擇後
我會幫你排除一個數字(絕對不會排除到上面已記錄的數字)
你可以任意選擇是否要更換(我建議為了方便是統一全部換獲全不不換 但不強迫)
你選擇完之後 我再公開密碼大家一起對答案 可以嗎?
簡單來說就是你一人分飾30腳同時平行進行一次三門問題實際演練
無題 無名 21/01/14(四)02:48:46 ID:kL3Ztoow No.2186064
>>2186062
所以你這裡就開始誤解了
沒有『後面的獎品會重新洗牌』這回事
如果後面的獎品會重新洗牌,先前的選門跟叫你換門就沒意義
3門1獎,中獎1門不會被重新洗牌
假設獎在A門,就到遊戲結束也會在A門,並不會改變
後面的獎品位置會被重置的話,就根本不乎合3門問題的模型
這樣已經被改成是其他數題了
所以你這裡就開始誤解了
沒有『後面的獎品會重新洗牌』這回事
如果後面的獎品會重新洗牌,先前的選門跟叫你換門就沒意義
3門1獎,中獎1門不會被重新洗牌
假設獎在A門,就到遊戲結束也會在A門,並不會改變
後面的獎品位置會被重置的話,就根本不乎合3門問題的模型
這樣已經被改成是其他數題了
>>2186062
繼續
因你已選取一門1/3是一組
你沒選的那兩扇門當一組,中獎率便是2/3
然後主持人會在你沒選的那兩扇門中開了有羊的門,但這其實沒有影響到,你沒選的那兩扇門是一組,中獎率是2/3的這個機率
更不應該把開了的羊門當成了不存在
因為你沒選的門,依然是兩扇門來的,中獎率依然是2/3
而你一開始選的門依然是中獎率1/3不變
如果把開了的羊門當成了不存在,就等於一開始就不存在
但請記住一開始你是3選1,所以開了的羊門絕不是一開始就不存在
所以這時主持人才問你要不要跟他換門
中獎率就是;
A:不換,中獎率就是一開始選門的1/3
B:換,中獎率就是那兩扇門那一組的2/3
繼續
因你已選取一門1/3是一組
你沒選的那兩扇門當一組,中獎率便是2/3
然後主持人會在你沒選的那兩扇門中開了有羊的門,但這其實沒有影響到,你沒選的那兩扇門是一組,中獎率是2/3的這個機率
更不應該把開了的羊門當成了不存在
因為你沒選的門,依然是兩扇門來的,中獎率依然是2/3
而你一開始選的門依然是中獎率1/3不變
如果把開了的羊門當成了不存在,就等於一開始就不存在
但請記住一開始你是3選1,所以開了的羊門絕不是一開始就不存在
所以這時主持人才問你要不要跟他換門
中獎率就是;
A:不換,中獎率就是一開始選門的1/3
B:換,中獎率就是那兩扇門那一組的2/3
無題 無名 21/01/14(四)03:55:55 ID:K/tfjuXc No.2186069
主持人洛克李:你們討論完了嗎?要不要換門?要打開囉!八門遁甲~開!
.
於是上面還繼續要跳針的島民都被揍了一頓
.
於是上面還繼續要跳針的島民都被揍了一頓
選A門-羊,換變成-車
選B門-羊,換變成-車
選C門-車,換變成-羊
別想太多,就是這麼簡單
關鍵字餵狗,很多網站可參考
可以不懂,但不會因為你堅持1/2而改變
https://ideone.com/fjJDGS
https://ideone.com/JY55fc
https://ideone.com/acJIxU
https://ideone.com/3dxXh7
選B門-羊,換變成-車
選C門-車,換變成-羊
別想太多,就是這麼簡單
關鍵字餵狗,很多網站可參考
可以不懂,但不會因為你堅持1/2而改變
https://ideone.com/fjJDGS
https://ideone.com/JY55fc
https://ideone.com/acJIxU
https://ideone.com/3dxXh7
無題 無名 21/01/14(四)04:52:58 ID:B3ST0zxE No.2186074
三門問題永遠都會討論不完
因為解釋的人為了讓人容易理解
就會打算改題目,比如改成100門
或是改成另一個問法:
選了其中一個門之後,主持人直接問你要不要換成開剩下的兩扇?
只要剩下的兩扇有開出一台車,那台車就是你的
題目改成這樣的話,也可以理解答案會是2/3
你可以有更多方式改問題,讓三門更好理解
但是,你怎麼能保證原本不懂的人
理解改過的問題之後,能夠接著同理可證三門問題
而不是指責你因為改了問題機率才會變那樣?
這就是為什麼網路辯論中
最忌諱的就是舉例
對方永遠有辦法對你的舉例雞蛋裡挑骨頭
因為解釋的人為了讓人容易理解
就會打算改題目,比如改成100門
或是改成另一個問法:
選了其中一個門之後,主持人直接問你要不要換成開剩下的兩扇?
只要剩下的兩扇有開出一台車,那台車就是你的
題目改成這樣的話,也可以理解答案會是2/3
你可以有更多方式改問題,讓三門更好理解
但是,你怎麼能保證原本不懂的人
理解改過的問題之後,能夠接著同理可證三門問題
而不是指責你因為改了問題機率才會變那樣?
這就是為什麼網路辯論中
最忌諱的就是舉例
對方永遠有辦法對你的舉例雞蛋裡挑骨頭
無題 無名 21/01/14(四)05:42:14 ID:fbvGYROk No.2186076
>>2186073
https://web.math.sinica.edu.tw/life_info/mathgame/montyhall/montyhall.html
https://web.math.sinica.edu.tw/life_info/mathgame/montyhall/montyhall.html
“If someone doesn't value evidence, what evidence are you going to provide to prove that they should value it? If someone doesn’t value logic, what logical argument could you provide to show the importance of logic?”
― Sam Harris
― Sam Harris
>>2186066
很有邏輯,卻依然偷換概念
我直接拿你們最愛的100門來講:
你一開始選、中獎率1/100~主持人扣掉其中的98/100個miss=你換了之後有99/100個中獎率
關鍵1=你一開始抽到什麼?
很多人在此時用機率說服大家「你一開始抽到miss是99/100,所以換門機率高達98/100」
卻無視你一開始就抽到獎,而且不斷告訴你1/100絕對比99/100難中的邏輯來洗腦你
關鍵2=接下來內容要連結上面的關鍵1就直接打臉100門論,你一開始抽到什麼?未知、但主持人接下來一定有98個miss會開啟(因為他一定知道,而這是固定要素),再來給你一次選擇權
聽到了嗎?主持人「再給你一次選擇權」的同時,你的1/100機率已經不存在了;這才是後半段的邏輯,主持人說再給你一次「選擇權」就是機率的分水嶺
也有人會說:前面你選是1/100;後面你再選不就是1/2;那換了之後1/2還是比1/100容易中啊??
其實答案已經你說到了,主持人的舉動已經改變機率邏輯,所以你在主持人行動後的眼前只有兩個門,換、不換都是1/2
很有邏輯,卻依然偷換概念
我直接拿你們最愛的100門來講:
你一開始選、中獎率1/100~主持人扣掉其中的98/100個miss=你換了之後有99/100個中獎率
關鍵1=你一開始抽到什麼?
很多人在此時用機率說服大家「你一開始抽到miss是99/100,所以換門機率高達98/100」
卻無視你一開始就抽到獎,而且不斷告訴你1/100絕對比99/100難中的邏輯來洗腦你
關鍵2=接下來內容要連結上面的關鍵1就直接打臉100門論,你一開始抽到什麼?未知、但主持人接下來一定有98個miss會開啟(因為他一定知道,而這是固定要素),再來給你一次選擇權
聽到了嗎?主持人「再給你一次選擇權」的同時,你的1/100機率已經不存在了;這才是後半段的邏輯,主持人說再給你一次「選擇權」就是機率的分水嶺
也有人會說:前面你選是1/100;後面你再選不就是1/2;那換了之後1/2還是比1/100容易中啊??
其實答案已經你說到了,主持人的舉動已經改變機率邏輯,所以你在主持人行動後的眼前只有兩個門,換、不換都是1/2
無題 無名 21/01/14(四)07:51:37 ID:AMZ.ejuM No.2186085
>>2186078
主持人篩選門有兩種可能的目的:
1.你第一次中了車,他就用另外一道門來唬爛你換門(1/3)
2.你第一次中了羊,他不得已只好篩掉另一頭羊來留下車(2/3)
你的第一次選擇不是沒用,因為主持人的行動不是隨便開掉另一扇門,假設你中了車,他篩門才會變得無關緊要
兩頭羊篩掉哪個都一樣,不過是誤導
但你第一次中羊的狀況下,主持人會被迫篩掉剩下的另一隻羊,使主持人留下的那道門有很高機率是車
主持人篩選門有兩種可能的目的:
1.你第一次中了車,他就用另外一道門來唬爛你換門(1/3)
2.你第一次中了羊,他不得已只好篩掉另一頭羊來留下車(2/3)
你的第一次選擇不是沒用,因為主持人的行動不是隨便開掉另一扇門,假設你中了車,他篩門才會變得無關緊要
兩頭羊篩掉哪個都一樣,不過是誤導
但你第一次中羊的狀況下,主持人會被迫篩掉剩下的另一隻羊,使主持人留下的那道門有很高機率是車
但是他有給你"再選一次剩下的那兩個門"的機會
那一開始的第一選是1/3機率
在可以第二選時沒參考價值
那一開始的第一選是1/3機率
在可以第二選時沒參考價值
無題 無名 21/01/14(四)08:25:35 ID:AMZ.ejuM No.2186091
>>2186089
第一次選擇其實很重要
因為它會限制主持人能開哪幾道門
在第一次就選到車的狀態下,主持人有兩個選擇可以選,不論開哪道對他來說都沒差
但第一次就選到羊的狀況下,主持人的選擇會被限縮在剩下的那隻羊,被強迫留下車的那道門,這也是造成為何換門不是純粹的1/2的緣故
當門越多,這個現象就會越明顯,因為只要你第一次沒選中,主持人就被迫要留下有車的門
第一次選擇其實很重要
因為它會限制主持人能開哪幾道門
在第一次就選到車的狀態下,主持人有兩個選擇可以選,不論開哪道對他來說都沒差
但第一次就選到羊的狀況下,主持人的選擇會被限縮在剩下的那隻羊,被強迫留下車的那道門,這也是造成為何換門不是純粹的1/2的緣故
當門越多,這個現象就會越明顯,因為只要你第一次沒選中,主持人就被迫要留下有車的門
無題 無名 21/01/14(四)08:26:57 ID:HMrKbidE No.2186092
無題 無名 21/01/14(四)08:34:15 ID:Lk805DTk No.2186095
>>2186093
That's not how the meme works
That's not how the meme works
你接受了旁白的說法
把兩個不相干的題
當作一個
並且被旁白的一句話說"第二題這樣想是錯的"
"你要去想如果門更多時會更有趣喔"
把兩個不相干的題
當作一個
並且被旁白的一句話說"第二題這樣想是錯的"
"你要去想如果門更多時會更有趣喔"
>>2186078
既然要用100門來討論,那就這麼設定吧
把所有門口編號,1~100,車子在門100後
玩家先選門,主持人介入後,玩家正式開門(不論換或不換),所有「會中車」的情況只有以下:
選1開100(換)
選2開100(換)
選3開100(換)
選4開100(換)
...
...
選99開100(換)
以上有99種
選100開100(不換)
以上有1種
你還是覺得換門的中獎率不會比較高?
當然啦,你現在的論點就是硬要分割前半的行動對「整個遊戲、從玩家剛走進會場、在他第一次選擇之前開始計算的中獎機率」造成的改變
然後說「遊戲機率要從後半段,也就是主持人干預過之後」開始起算,所以機率對玩家來講就是2扇門選一扇,所以是1/2
那我只能說,我們是在平行時空討論問題,你的問題不是我的問題
既然要用100門來討論,那就這麼設定吧
把所有門口編號,1~100,車子在門100後
玩家先選門,主持人介入後,玩家正式開門(不論換或不換),所有「會中車」的情況只有以下:
選1開100(換)
選2開100(換)
選3開100(換)
選4開100(換)
...
...
選99開100(換)
以上有99種
選100開100(不換)
以上有1種
你還是覺得換門的中獎率不會比較高?
當然啦,你現在的論點就是硬要分割前半的行動對「整個遊戲、從玩家剛走進會場、在他第一次選擇之前開始計算的中獎機率」造成的改變
然後說「遊戲機率要從後半段,也就是主持人干預過之後」開始起算,所以機率對玩家來講就是2扇門選一扇,所以是1/2
那我只能說,我們是在平行時空討論問題,你的問題不是我的問題
無題 無名 21/01/14(四)09:45:47 ID:vnLG2V4s No.2186115
>>2186112
旁白的問題干我屁事.jpg
旁白的問題干我屁事.jpg
>>2186078
>>2186096
也還真是奇葩
頭一次看到放大到100門還是不理解的人
放到100門一般人本該就意識到1/2是錯在那裡…
你們卡住的地方,就是誤以為主持人問你換與不換門,是一個重新洗牌的選項
這樣想的話,你們才是被主持人誤導
因為這不是一個自由洗牌選項,正確來說,
主持人是在問你要不要換走你手上原有機率的那扇門
100門的話,不換門能中車的可能性,只有你在一開始的100門中一次就選中車,也就是說只有百分之一的可能性
再注意不是隨意選一邊,而是換走不換走你一開始已選的門
假設我不換門,中車的可能性就是只有百分之一(1/100)
所以我就是選不換門結束這回合,能中的就是1/100
既然不換中車的可能性是1/100
那來換與不換中車的可能性都是1/2!?
最後我要再放個大絕
https://www.google.com/url?sa=t&source=web&rct=j&url=https://science.km.edu.tw/storage/media/332/58d6a4c27dfa4.pdf&ved=2ahUKEwjultLF75juAhWLxYsBHRwrC3MQFjAAegQIARAB&usg=AOvVaw3csThMeVHQ6pPLV9NkVKU6
這是小學生做的驗證比率圖,麻煩你們自己看看,裡面換門的話,中車率有沒有比較高?還是你們說的中車率都是1/2?
>>2186096
也還真是奇葩
頭一次看到放大到100門還是不理解的人
放到100門一般人本該就意識到1/2是錯在那裡…
你們卡住的地方,就是誤以為主持人問你換與不換門,是一個重新洗牌的選項
這樣想的話,你們才是被主持人誤導
因為這不是一個自由洗牌選項,正確來說,
主持人是在問你要不要換走你手上原有機率的那扇門
100門的話,不換門能中車的可能性,只有你在一開始的100門中一次就選中車,也就是說只有百分之一的可能性
再注意不是隨意選一邊,而是換走不換走你一開始已選的門
假設我不換門,中車的可能性就是只有百分之一(1/100)
所以我就是選不換門結束這回合,能中的就是1/100
既然不換中車的可能性是1/100
那來換與不換中車的可能性都是1/2!?
最後我要再放個大絕
https://www.google.com/url?sa=t&source=web&rct=j&url=https://science.km.edu.tw/storage/media/332/58d6a4c27dfa4.pdf&ved=2ahUKEwjultLF75juAhWLxYsBHRwrC3MQFjAAegQIARAB&usg=AOvVaw3csThMeVHQ6pPLV9NkVKU6
這是小學生做的驗證比率圖,麻煩你們自己看看,裡面換門的話,中車率有沒有比較高?還是你們說的中車率都是1/2?
>>2186108
所以我就說別偷換概念,你硬是要把「中與不中」的2選1=1/2,蓋過「兩個選擇其中一個」的1/2的概念就省省吧
這就是邏輯問題,但永遠有人列出一票公式想掩蓋後面的邏輯,這不是平行世界、而是在偷換概念
你想把分母無限大到N都無所謂,你想列的數學公式也是正確;
但是邏輯不是只有這樣,只因為後面還多了新的邏輯就直接推翻
我拿最簡單的邏輯打臉:
A=B,B=C,A=C
這邏輯想推翻的儘管來
接著我要重述一次問題:
你眼前有三道門→你選一個→主持人把剩下兩個的其中一道門打開而且必定是miss→你有一次選擇換與不換(*)
我把以上問題與流程當作A
然後在上面主持人的行動後再給你選擇的(*)條件時,你的中獎率就是1/2,這是鐵率
也就是我說的「當你在作第二次選擇時,前面的任何條件與公式都已經被打臉了」所以最後你面對的永遠是「你眼前剩下兩道門,無論你換不換,只有一個有獎而另一個是miss」
到這邊還是無法理解的,只能說你有邏輯、但無法分辨所以被偷換概念
所以我就說別偷換概念,你硬是要把「中與不中」的2選1=1/2,蓋過「兩個選擇其中一個」的1/2的概念就省省吧
這就是邏輯問題,但永遠有人列出一票公式想掩蓋後面的邏輯,這不是平行世界、而是在偷換概念
你想把分母無限大到N都無所謂,你想列的數學公式也是正確;
但是邏輯不是只有這樣,只因為後面還多了新的邏輯就直接推翻
我拿最簡單的邏輯打臉:
A=B,B=C,A=C
這邏輯想推翻的儘管來
接著我要重述一次問題:
你眼前有三道門→你選一個→主持人把剩下兩個的其中一道門打開而且必定是miss→你有一次選擇換與不換(*)
我把以上問題與流程當作A
然後在上面主持人的行動後再給你選擇的(*)條件時,你的中獎率就是1/2,這是鐵率
也就是我說的「當你在作第二次選擇時,前面的任何條件與公式都已經被打臉了」所以最後你面對的永遠是「你眼前剩下兩道門,無論你換不換,只有一個有獎而另一個是miss」
到這邊還是無法理解的,只能說你有邏輯、但無法分辨所以被偷換概念
無題 無名 21/01/14(四)10:32:08 ID:aWpntNzI No.2186124
無題 無名 21/01/14(四)10:33:25 ID:vnLG2V4s No.2186125
無題 無名 21/01/14(四)10:41:19 ID:CPnbn4qI No.2186127
所以
我們為何要為智障解釋這樣多?
我們為何要為智障解釋這樣多?
無題 無名 21/01/14(四)10:45:38 ID:oRvAT/Tg No.2186129
無題 無名 21/01/14(四)11:02:47 ID:aWpntNzI No.2186145
無題 無名 21/01/14(四)11:04:08 ID:yOVNiZ.E No.2186146
無題 無名 21/01/14(四)11:04:17 ID:72iTPPl2 No.2186147
因為主持人開的一定是沒中獎的門
"換門"和"選第一扇之外所有的門"是等價的
並不是二選一
"換門"和"選第一扇之外所有的門"是等價的
並不是二選一
無題 無名 21/01/14(四)11:05:12 ID:FdGAVkO6 No.2186148
無題 無名 21/01/14(四)11:13:11 ID:vFXlNnHc No.2186154
>>2186153
歹勢,沒仔細看(死
歹勢,沒仔細看(死
無題 無名 21/01/14(四)11:20:55 ID:FdGAVkO6 No.2186156
>>2186139
再看看這篇有熊老師的詳解
https://medium.com/@tpdjdje0525/毒蛙問題-山羊-or-汽車-蒙提霍爾問題-88c0f427fec2
希望有助你能從幼稚園畢業升上小學吧
再看看這篇有熊老師的詳解
https://medium.com/@tpdjdje0525/毒蛙問題-山羊-or-汽車-蒙提霍爾問題-88c0f427fec2
希望有助你能從幼稚園畢業升上小學吧
無題 無名 21/01/14(四)11:26:54 ID:LaAQSF6. No.2186160
>>2186125
你這樣子叫偽命題
我知道機率這種東西很抽象
但是用數學來討論現實物理現象時,時間常數(t)必須為正
因為題目已經告訴你結果了,所以很多人都會習慣逆向推論
但是機率你不可以用已知的結果來逆向推論,這樣你的時間常數(t)就會是負的
除非你今天跟我說你會穿越時間,你再來討論
你這樣子叫偽命題
我知道機率這種東西很抽象
但是用數學來討論現實物理現象時,時間常數(t)必須為正
因為題目已經告訴你結果了,所以很多人都會習慣逆向推論
但是機率你不可以用已知的結果來逆向推論,這樣你的時間常數(t)就會是負的
除非你今天跟我說你會穿越時間,你再來討論
>>2186141
假設現在有100枚硬幣 無論是外型、大小、重量皆相同
但其中一枚是刻有伊莉莎白二世的金幣
現在主持人要你在蒙眼的情況下挑一枚握在手中
接著把其他98枚普通硬幣排除掉 問你要不要更換選擇
因為你已經把一枚硬幣握在手中了 所以主持人排除硬幣時是不會影響到你手中那枚硬幣的
在這種情況下 除非你在一開始就抓住1/100的機率把金幣握在手中
否則剩下那枚未知硬幣是金幣的機率就是99/100
假設現在有100枚硬幣 無論是外型、大小、重量皆相同
但其中一枚是刻有伊莉莎白二世的金幣
現在主持人要你在蒙眼的情況下挑一枚握在手中
接著把其他98枚普通硬幣排除掉 問你要不要更換選擇
因為你已經把一枚硬幣握在手中了 所以主持人排除硬幣時是不會影響到你手中那枚硬幣的
在這種情況下 除非你在一開始就抓住1/100的機率把金幣握在手中
否則剩下那枚未知硬幣是金幣的機率就是99/100
無論怎麼辯解,換了之後機率變大的可能性必須要有以下兩點才能成立:
1.你需要用主持人=上帝視角來面對這個過程,而且主持人必須要知道並且排除剩下的miss
2.在以上動作之後,你有換不換的選擇權
假如說今天題目少了「第二次的選擇權」,那麼這一切都存在;
但今天依然有人拿公式來說服他人「換了才好」,就是因為題目中有著「主持人知道全部答案」+「主持人淘汰掉其他miss只留一個miss」這個盲點來成立各位的錯覺
如果主持人「並不知道全部的答案而淘汰到剩下兩個門」那機率結果就不同了;
而更有趣的是就算是這個發展下你還有第二次選擇權時,結果又會回到1/2
這邊可不是說「中與不中」的二擇結果的1/2
,而是主持人一連串動作後,「你眼前只會剩下2個門、接著你有選擇權」
有邏輯的人就能明白現在發生了什麼事,沒錯,這就像是「一開始你眼前有兩道門、一個有獎一個miss、然後你選一個」
我並沒有偷換概念哦,而是陳述題目中最後發展的事實,
所以一堆人都被那些啥公式的給騙到盲點,真正在你進入第二次選擇時,你就只會是1/2,1代表獎品或是miss,2代表兩個門
選後機率高,只有必須成立於「你沒有第二次的選擇權」,很矛盾、卻也是邏輯
因為這個「機率高」就是你用主持人=上帝視角才能成立的
否則你再仔細想想:你一開始的選擇是1/n,但主持人打掉其他miss後讓現場只剩獎品與miss共兩個門的行動後,你再作選擇…………………你還在說不是1/2?
1.你需要用主持人=上帝視角來面對這個過程,而且主持人必須要知道並且排除剩下的miss
2.在以上動作之後,你有換不換的選擇權
假如說今天題目少了「第二次的選擇權」,那麼這一切都存在;
但今天依然有人拿公式來說服他人「換了才好」,就是因為題目中有著「主持人知道全部答案」+「主持人淘汰掉其他miss只留一個miss」這個盲點來成立各位的錯覺
如果主持人「並不知道全部的答案而淘汰到剩下兩個門」那機率結果就不同了;
而更有趣的是就算是這個發展下你還有第二次選擇權時,結果又會回到1/2
這邊可不是說「中與不中」的二擇結果的1/2
,而是主持人一連串動作後,「你眼前只會剩下2個門、接著你有選擇權」
有邏輯的人就能明白現在發生了什麼事,沒錯,這就像是「一開始你眼前有兩道門、一個有獎一個miss、然後你選一個」
我並沒有偷換概念哦,而是陳述題目中最後發展的事實,
所以一堆人都被那些啥公式的給騙到盲點,真正在你進入第二次選擇時,你就只會是1/2,1代表獎品或是miss,2代表兩個門
選後機率高,只有必須成立於「你沒有第二次的選擇權」,很矛盾、卻也是邏輯
因為這個「機率高」就是你用主持人=上帝視角才能成立的
否則你再仔細想想:你一開始的選擇是1/n,但主持人打掉其他miss後讓現場只剩獎品與miss共兩個門的行動後,你再作選擇…………………你還在說不是1/2?
無題 無名 21/01/14(四)12:01:07 ID:Y.HfPYQE No.2186171
那換個問題,如果是選完一扇門
主持人再打開另一扇門,門後是車子的機率是多少?
主持人再打開另一扇門,門後是車子的機率是多少?
無題 無名 21/01/14(四)12:04:46 ID:oRvAT/Tg No.2186173
無題 無名 21/01/14(四)12:05:41 ID:Gu8ASCtU No.2186174
>>2186125
列舉事件就好了
假設1號是獎品
1 不換 中
1 換 沒中
2 不換 沒中
2 換 中
3 不換 沒中
3 換 中
如果你的第二次選擇行為是當場才隨機擲硬幣決定換或是不換
那機率確實是50%
如果你的行為是一定換,完全不考慮不換
1 換 沒中
2 換 中
3 換 中
那機率是2/3
列舉事件就好了
假設1號是獎品
1 不換 中
1 換 沒中
2 不換 沒中
2 換 中
3 不換 沒中
3 換 中
如果你的第二次選擇行為是當場才隨機擲硬幣決定換或是不換
那機率確實是50%
如果你的行為是一定換,完全不考慮不換
1 換 沒中
2 換 中
3 換 中
那機率是2/3
>>2186170
當然不是1/2 用我上面的例子來說
你已經把一枚硬幣握在手中了 主持人是無法干涉這枚硬幣的
意即你手中的硬幣自始至終都是1/100機率金幣
主持人排除的是“你手中以外的其他98枚普通硬幣“
也就是說
>>除非你在一開始就抓住1/100的機率把金幣握在手中 否則剩下那枚未知硬幣是金幣的機率就是99/100
當然不是1/2 用我上面的例子來說
你已經把一枚硬幣握在手中了 主持人是無法干涉這枚硬幣的
意即你手中的硬幣自始至終都是1/100機率金幣
主持人排除的是“你手中以外的其他98枚普通硬幣“
也就是說
>>除非你在一開始就抓住1/100的機率把金幣握在手中 否則剩下那枚未知硬幣是金幣的機率就是99/100
>>2186166
換了題目也改變不了結果,
你一開始拿到金幣→主持人去掉其他銀幣只留一個→你再選擇
跟
你選到銀幣→主持人拿掉其他銀幣只留金幣→你再選一次
結果的機率一樣
看到沒,我說了,這一切都必須成立在主持人視點淘汰掉miss、讓現場「一定剩下一個獎與一個miss」
這就是關鍵1,假如主持人也不知情的情況下淘汰到現場剩兩個(一個是你先選的)那麼你換了之後有提升獎品機率?答案是否
而中獎機率1/2的成立,就是在於「現場有兩個、一個獎、一個miss、你作選擇」
與原始題目差別在於主持人淘汰掉其他的miss讓「現場有兩個」門、然後你最後有第二次的「選擇」
換了題目也改變不了結果,
你一開始拿到金幣→主持人去掉其他銀幣只留一個→你再選擇
跟
你選到銀幣→主持人拿掉其他銀幣只留金幣→你再選一次
結果的機率一樣
看到沒,我說了,這一切都必須成立在主持人視點淘汰掉miss、讓現場「一定剩下一個獎與一個miss」
這就是關鍵1,假如主持人也不知情的情況下淘汰到現場剩兩個(一個是你先選的)那麼你換了之後有提升獎品機率?答案是否
而中獎機率1/2的成立,就是在於「現場有兩個、一個獎、一個miss、你作選擇」
與原始題目差別在於主持人淘汰掉其他的miss讓「現場有兩個」門、然後你最後有第二次的「選擇」
>>2186175
然後第二次選擇咧?
當存在第二次選擇時的時間點的時候,你提的前面原定的機率就已經沒意義了
只要沒有第二次選擇,那對主持人來說當然是後者機率大,但站在參賽者的立場時,第二次選擇的時間點就條件一切改變了
然後第二次選擇咧?
當存在第二次選擇時的時間點的時候,你提的前面原定的機率就已經沒意義了
只要沒有第二次選擇,那對主持人來說當然是後者機率大,但站在參賽者的立場時,第二次選擇的時間點就條件一切改變了
無題 無名 21/01/14(四)12:15:57 ID:x69CsGmQ No.2186180
無題 無名 21/01/14(四)12:16:16 ID:LaAQSF6. No.2186181
>>2186170
就說了機率不能逆推了RRR....
我剛剛不是用公式也不是舉例那幾百個門的樣本
就只是單純的討論物理現象而已,有這麼難懂嗎
你不能用後來知道的"中獎品"與"沒中獎品"來當作1/2逆推回去啊
你這樣逆推回去機率當然會變成1/2啊
但是你的時間會是負的嗎?你會時間開倒車嗎?你是克里姆王喔?
就說了機率不能逆推了RRR....
我剛剛不是用公式也不是舉例那幾百個門的樣本
就只是單純的討論物理現象而已,有這麼難懂嗎
你不能用後來知道的"中獎品"與"沒中獎品"來當作1/2逆推回去啊
你這樣逆推回去機率當然會變成1/2啊
但是你的時間會是負的嗎?你會時間開倒車嗎?你是克里姆王喔?
無題 無名 21/01/14(四)12:18:57 ID:yOVNiZ.E No.2186182
看吧,這些還在那邊說1/2的白痴們是無法理解的
他們的腦袋就只能理解:剩下兩個門所以是1/2
他們甚至連google蒙提霍爾問題都不會
被證實幾十年的理論,他們可以只憑直覺就反對
而且還說得振振有詞www
這個社會是有人才跟蠢材的
不用浪費時間去跟蠢材爭論
還是需要這些蠢材去做不用腦的低端工作
這社會才能持續運轉
他們的腦袋就只能理解:剩下兩個門所以是1/2
他們甚至連google蒙提霍爾問題都不會
被證實幾十年的理論,他們可以只憑直覺就反對
而且還說得振振有詞www
這個社會是有人才跟蠢材的
不用浪費時間去跟蠢材爭論
還是需要這些蠢材去做不用腦的低端工作
這社會才能持續運轉
無題 無名 21/01/14(四)12:57:44 ID:FdGAVkO6 No.2186194
無題 無名 21/01/14(四)12:58:21 ID:vFXlNnHc No.2186196
>>2186193
你應該把你文中的"我"換成"你"
你應該把你文中的"我"換成"你"
無題 無名 21/01/14(四)13:02:30 ID:ONwS3nMI No.2186198
>>2186193
你真棒
你真棒
>>2186177
所以說…… 維基寫錯了……嗎?
我可以直接告訴你,維基是對的。
而且我可以告訴你,「科學家用電腦模疑過幾千次後,發現「選擇換,得到汽車的機率,真的是 2/3」
這不科學啊!
好吧,那我再多說一句,除了模擬結果的「現實」是如此,其實從其「原理」上推論,也應該是 2/3 ……
也就是說,上面張圖,其實有錯…… 錯在哪裡呢? 你能想到嗎?
所以說…… 維基寫錯了……嗎?
我可以直接告訴你,維基是對的。
而且我可以告訴你,「科學家用電腦模疑過幾千次後,發現「選擇換,得到汽車的機率,真的是 2/3」
這不科學啊!
好吧,那我再多說一句,除了模擬結果的「現實」是如此,其實從其「原理」上推論,也應該是 2/3 ……
也就是說,上面張圖,其實有錯…… 錯在哪裡呢? 你能想到嗎?
>>2186218
條件機率的應用問題,不只是學生常錯,就連老師也可能會解錯 — 通常都是因為,搞不清楚現實問題中的「條件」是什麼。
比如說,「蒙提霍爾問題」 就「不是」條件機率的問題……
蛤? 真的嗎?
那「已知主持人打開的門裡是羊」呢? 這不是條件,那什麼才是條件?
— 沒錯,問題就在於「什麼才是條件?」
可以這麼說「條件機率」 的所謂 “條件”,其實「觀察條件 (資訊)」 — 也就是樣本已經發生了,但你只針對其中的「符合觀察條件 (事件B)的一部份」,觀察這部份裡,「屬於事件A的,占多少」;
這樣,算作「已知事件B發生,則事件A發生的機率」= P(A|B)
但「蒙提霍爾問題」 裡面, 「主持人不開你選的那扇門」和「主持人不開有車的那扇門」, 並不是「你觀察的條件」,而是「樣本產生 (實驗操作) 的改變」。
觀察條件:
「你隨機選、主持人隨機開門,已知主持人打開的門是山羊」 ,則選擇「換」或不換,得到汽車的機率都是 1/2 — 像上面的圖所說明的。
操作改變:
「你隨機選、主持人不開你選的那扇、也不開有車的那扇」,則選擇「換」得到汽車的機率會是 2/3 (選「不換」則只有 1/3)
條件機率的應用問題,不只是學生常錯,就連老師也可能會解錯 — 通常都是因為,搞不清楚現實問題中的「條件」是什麼。
比如說,「蒙提霍爾問題」 就「不是」條件機率的問題……
蛤? 真的嗎?
那「已知主持人打開的門裡是羊」呢? 這不是條件,那什麼才是條件?
— 沒錯,問題就在於「什麼才是條件?」
可以這麼說「條件機率」 的所謂 “條件”,其實「觀察條件 (資訊)」 — 也就是樣本已經發生了,但你只針對其中的「符合觀察條件 (事件B)的一部份」,觀察這部份裡,「屬於事件A的,占多少」;
這樣,算作「已知事件B發生,則事件A發生的機率」= P(A|B)
但「蒙提霍爾問題」 裡面, 「主持人不開你選的那扇門」和「主持人不開有車的那扇門」, 並不是「你觀察的條件」,而是「樣本產生 (實驗操作) 的改變」。
觀察條件:
「你隨機選、主持人隨機開門,已知主持人打開的門是山羊」 ,則選擇「換」或不換,得到汽車的機率都是 1/2 — 像上面的圖所說明的。
操作改變:
「你隨機選、主持人不開你選的那扇、也不開有車的那扇」,則選擇「換」得到汽車的機率會是 2/3 (選「不換」則只有 1/3)
無題 無名 21/01/14(四)14:36:14 ID:aWpntNzI No.2186221
>>2186220
… … 真的嗎? 真的是差在這嗎?
如果你對我的說法有所懷疑,那你已經邁出了第一步了…… 但這還不夠,你要 試著把自己的念頭想完整!
不過,為了鼓勵你,這次就由我代勞吧:
我們就以最最基本的「一位母親,生了三個小孩」來作範例吧:附圖
這樣有懂了嗎?
-- 必須是樣本已經產生了,但我「只 觀察 符合某些條件」的標的,才能用條件機率;
-- 如果是樣本產生的過程,本身就有某些「操作改變」,那就不能算是條件機率。
… … 真的嗎? 真的是差在這嗎?
如果你對我的說法有所懷疑,那你已經邁出了第一步了…… 但這還不夠,你要 試著把自己的念頭想完整!
不過,為了鼓勵你,這次就由我代勞吧:
我們就以最最基本的「一位母親,生了三個小孩」來作範例吧:附圖
這樣有懂了嗎?
-- 必須是樣本已經產生了,但我「只 觀察 符合某些條件」的標的,才能用條件機率;
-- 如果是樣本產生的過程,本身就有某些「操作改變」,那就不能算是條件機率。
無題 無名 21/01/14(四)15:10:31 ID:B3ST0zxE No.2186227
>>2186176
你誤解了一點
蒙提霍爾問題討論的是總是換或總是不換的機率差異
所以換或不換不是選擇,而是兩個狀況
你總是換->換到車的機率是2/3
你總是不換->選到車的機率是1/3
你把換或不換誤當作選擇
意即誤以為參加者會隨機從換或不換之中選一個
才會誤以為獲得車的機率是1/2
你誤解了一點
蒙提霍爾問題討論的是總是換或總是不換的機率差異
所以換或不換不是選擇,而是兩個狀況
你總是換->換到車的機率是2/3
你總是不換->選到車的機率是1/3
你把換或不換誤當作選擇
意即誤以為參加者會隨機從換或不換之中選一個
才會誤以為獲得車的機率是1/2
無題 無名 21/01/14(四)15:35:22 ID:PxEKtYmk No.2186236
我們來一步步解析
步驟1
玩家三選一
步驟2
主持人開一扇門(規則規定主持人必須知道門後的內容並且打開有羊的門)
步驟3
主持人詢問玩家是否要換門
步驟4
決定完畢後開門開獎
現在讓我們一個一個步驟解析
有一件很重要的事情要一開始就充分認知
玩家跟主持人從一開始就是不同的
所以他們可以得到的資訊範圍完全不同
步驟1
在玩家已知情報範圍
沒有任何情報下隨機選擇一扇門的中獎率很顯然是1/3
但是換成主持人視角
他已經知道玩家現在有沒有中獎了
步驟2
此步驟一開始
三扇門被分為兩組
組別1 玩家一開始選中的一扇門
組別2 玩家沒有選中的兩扇門
由於遊戲規則定義 主持人必須在組別2中挑選一扇未中獎門開啟展示
不管玩家一開始是否有選中
主持人開啟一扇未中獎門 此事件發生機率為100%
所以此步驟實質沒有意義只是單純的障眼法
步驟3
主持人詢問是否交換
實質上就是玩家要不用用一開始選擇的組別1跟主持人交換組別2
機率在一開始選擇的時候就被分為獨立的兩組了
步驟1
玩家三選一
步驟2
主持人開一扇門(規則規定主持人必須知道門後的內容並且打開有羊的門)
步驟3
主持人詢問玩家是否要換門
步驟4
決定完畢後開門開獎
現在讓我們一個一個步驟解析
有一件很重要的事情要一開始就充分認知
玩家跟主持人從一開始就是不同的
所以他們可以得到的資訊範圍完全不同
步驟1
在玩家已知情報範圍
沒有任何情報下隨機選擇一扇門的中獎率很顯然是1/3
但是換成主持人視角
他已經知道玩家現在有沒有中獎了
步驟2
此步驟一開始
三扇門被分為兩組
組別1 玩家一開始選中的一扇門
組別2 玩家沒有選中的兩扇門
由於遊戲規則定義 主持人必須在組別2中挑選一扇未中獎門開啟展示
不管玩家一開始是否有選中
主持人開啟一扇未中獎門 此事件發生機率為100%
所以此步驟實質沒有意義只是單純的障眼法
步驟3
主持人詢問是否交換
實質上就是玩家要不用用一開始選擇的組別1跟主持人交換組別2
機率在一開始選擇的時候就被分為獨立的兩組了
這串沉了嗎
終於沉沒了
那我來最後總結一下
結論就是
這意味你們都是GAY..........
停
認真講
怎麼沒人想到也許這跟量子實驗一樣
當有主持人再問跟觀測你反應時
機率就跟你直接挑一個門打開會不一樣呢
沒錯
你應該理解
門打開後只有兩個結果
那就是一切事實真相了
終於沉沒了
那我來最後總結一下
結論就是
這意味你們都是GAY..........
停
認真講
怎麼沒人想到也許這跟量子實驗一樣
當有主持人再問跟觀測你反應時
機率就跟你直接挑一個門打開會不一樣呢
沒錯
你應該理解
門打開後只有兩個結果
那就是一切事實真相了
無題 無名 21/01/14(四)18:51:08 ID:kL3Ztoow No.2186272
>>2186268
這就是著名的量子力學思想實驗:薛仁貴東征
這就是著名的量子力學思想實驗:薛仁貴東征
無題 無名 21/01/14(四)21:21:26 ID:PxEKtYmk No.2186296
>>2186295
你是故意來亂的對吧
你列出了選擇換門下的所有事件
但是在遊戲規則下
>第一次選中B 換門=得A
>第一次選中A 換門=得B
這兩個事件事不能發生的
然後因為有條件限制的關係 所有可能性並非真隨機
會受條件影響而讓機率並非均勻的分佈在所有可能性中
你是故意來亂的對吧
你列出了選擇換門下的所有事件
但是在遊戲規則下
>第一次選中B 換門=得A
>第一次選中A 換門=得B
這兩個事件事不能發生的
然後因為有條件限制的關係 所有可能性並非真隨機
會受條件影響而讓機率並非均勻的分佈在所有可能性中
第一次選中車 換門=得A
第一次選中車 換門=得B
第一次選中車 不換門=得車
第一次選中車 不換門=得車
第一次選中A 不換門=得A
第一次選中A 換門=得車
第一次選中B 不換門=得B
第一次選中B 換門=得車
第一次選中車 換門=得B
第一次選中車 不換門=得車
第一次選中車 不換門=得車
第一次選中A 不換門=得A
第一次選中A 換門=得車
第一次選中B 不換門=得B
第一次選中B 換門=得車
給昨天那群嗆的很開心的「人類」
如果你們還是不懂「換門後中車」的機率和「門後有車」的機率
就去看這篇文章
https://mathpots.com/menu/main-course/monty-hall-problem/
當然你們也能找個數學系專家來反駁
如果你們還是不懂「換門後中車」的機率和「門後有車」的機率
就去看這篇文章
https://mathpots.com/menu/main-course/monty-hall-problem/
當然你們也能找個數學系專家來反駁
無題 無名 21/01/14(四)21:36:37 ID:PxEKtYmk No.2186300
>>2186298
>第一次選中車 換門=得A
>第一次選中車 換門=得B
>第一次選中車 不換門=得車
>第一次選中車 不換門=得車
>第一次選中A 不換門=得A
>第一次選中A 換門=得車
>第一次選中B 不換門=得B
>第一次選中B 換門=得車
我們先不要管換門不換門 有沒有中獎 只看第一次選擇
你羅列了8次遊戲過程 當中有4次你一開始選擇了車
因此在你羅列的數據中 第一次選中車的機率變成了1/2
你看了都不覺得有問題嗎?
>第一次選中車 換門=得A
>第一次選中車 換門=得B
>第一次選中車 不換門=得車
>第一次選中車 不換門=得車
>第一次選中A 不換門=得A
>第一次選中A 換門=得車
>第一次選中B 不換門=得B
>第一次選中B 換門=得車
我們先不要管換門不換門 有沒有中獎 只看第一次選擇
你羅列了8次遊戲過程 當中有4次你一開始選擇了車
因此在你羅列的數據中 第一次選中車的機率變成了1/2
你看了都不覺得有問題嗎?
第一次選中車 換門=得A/B
第一次選中車 不換門=得車
第一次選中A 不換門=得A
第一次選中A 換門=得車
第一次選中B 不換門=得B
第一次選中B 換門=得車
所以應該是這列嗎
第一次選中車 不換門=得車
第一次選中A 不換門=得A
第一次選中A 換門=得車
第一次選中B 不換門=得B
第一次選中B 換門=得車
所以應該是這列嗎
>>2186299
那張樹狀圖畫的是 主持人詢問是否選擇換門的時候
不是經由前面的資訊進行理性判斷 而是隨機選擇是否要換門的狀況有多大的機率會選擇哪扇門
你自己陷入了奇怪的邏輯誤區
並用著跟其他人截然不同的名詞定義在爭論
這樣子真的不會吵出個結果...
畢竟你或許沒錯 但你處在跟別人不同的頻率討論毫無交集
那張樹狀圖畫的是 主持人詢問是否選擇換門的時候
不是經由前面的資訊進行理性判斷 而是隨機選擇是否要換門的狀況有多大的機率會選擇哪扇門
你自己陷入了奇怪的邏輯誤區
並用著跟其他人截然不同的名詞定義在爭論
這樣子真的不會吵出個結果...
畢竟你或許沒錯 但你處在跟別人不同的頻率討論毫無交集
無題 無名 21/01/14(四)21:48:32 ID:kBZc5qiQ No.2186308
>>2186299
直覺的1/2是怎麼回事?
還是覺得1/2這個答案深深吸引你嗎?沒關係,我有一樣的感覺XD 看來我們不能獲邀去 Mickey的小圈圈了。
那麼關於1/2,究竟有沒有一個合理的解釋?答案是有的,由前面畫的樹狀圖其實可以看得出來。
這張圖就是前面樹狀圖的後半段,有發現後半的每個選擇機率都是1/2嗎?
也就是說,我們直覺會認為是1/2,是基於最後面的選擇問題(要換或是不換),所以這個直覺基本上沒錯,卻忽略了前面的條件:主持人知道答案且幫你開了其他道門。
這也恰恰是日常生活中很常出現的謬誤,一旦前面有條件發生,後面的事件機率就會產生巨大的改變,就像Ben說的:it changed everything.
幹你媽,你貼的這段不就說了覺得是1/2是個謬誤了嗎
直覺的1/2是怎麼回事?
還是覺得1/2這個答案深深吸引你嗎?沒關係,我有一樣的感覺XD 看來我們不能獲邀去 Mickey的小圈圈了。
那麼關於1/2,究竟有沒有一個合理的解釋?答案是有的,由前面畫的樹狀圖其實可以看得出來。
這張圖就是前面樹狀圖的後半段,有發現後半的每個選擇機率都是1/2嗎?
也就是說,我們直覺會認為是1/2,是基於最後面的選擇問題(要換或是不換),所以這個直覺基本上沒錯,卻忽略了前面的條件:主持人知道答案且幫你開了其他道門。
這也恰恰是日常生活中很常出現的謬誤,一旦前面有條件發生,後面的事件機率就會產生巨大的改變,就像Ben說的:it changed everything.
幹你媽,你貼的這段不就說了覺得是1/2是個謬誤了嗎
>>2186307
你理解錯了
那張圖是列出包含一開始選門,主持人開門,以及換門與否的所有結果
如果還是不能理解,就把門1換成車,門23換成羊代入
也就是你換與不換是車與羊的差別,這就是門後有車或羊的機率
然後不是我要提不同的東西
你自己看上面一堆垃圾用錯誤的方法教人
自創什麼一開始門後有車的機率是1/3,主持人開門之後門後有車的機率一樣是1/3的鬼邏輯
還瞎扯有羊那扇門開啟後,這扇門門後有車的機率一樣是1/3
你他x的是不是瞧不起機率,瞧不起數學?
你理解錯了
那張圖是列出包含一開始選門,主持人開門,以及換門與否的所有結果
如果還是不能理解,就把門1換成車,門23換成羊代入
也就是你換與不換是車與羊的差別,這就是門後有車或羊的機率
然後不是我要提不同的東西
你自己看上面一堆垃圾用錯誤的方法教人
自創什麼一開始門後有車的機率是1/3,主持人開門之後門後有車的機率一樣是1/3的鬼邏輯
還瞎扯有羊那扇門開啟後,這扇門門後有車的機率一樣是1/3
你他x的是不是瞧不起機率,瞧不起數學?
>>2186312
因為我們昨天談的是另外一件事
換門後中車的機率是2/3這點沒異議
然而上面有些人的解釋是
因為某扇門一開始門後有車的機率是1/3,所以主持人開門後,這扇門門後有車的機率一樣是1/3
1-1/3=2/3
然後問題來了
剩下2扇門門後有車的機率都是1/3,那剩下的1/3呢?
結果某個天才就說被開啟已知是羊的那扇門門後有車的機率也是1/3
WTF?
因為我們昨天談的是另外一件事
換門後中車的機率是2/3這點沒異議
然而上面有些人的解釋是
因為某扇門一開始門後有車的機率是1/3,所以主持人開門後,這扇門門後有車的機率一樣是1/3
1-1/3=2/3
然後問題來了
剩下2扇門門後有車的機率都是1/3,那剩下的1/3呢?
結果某個天才就說被開啟已知是羊的那扇門門後有車的機率也是1/3
WTF?
無題 無名 21/01/14(四)22:10:14 ID:PxEKtYmk No.2186316
我把圖翻譯成中文並稍微增加了一點點說明
此圖為一開始選擇1號門之後 隨機決定是否換門的所有狀況及發生率
值得關注的是主持人開門的環節 因為規則限制他不能開到有車的門
所以在下面兩個可能性中都各別被迫只能用100%的機率開啟2或3號門
這個環節就是造成後面機率分佈開始被打亂的原因 也就是增加了新的"條件"
我加上綠點的地方是最後有選到車的狀況 自己作點基本的計算吧
此圖為一開始選擇1號門之後 隨機決定是否換門的所有狀況及發生率
值得關注的是主持人開門的環節 因為規則限制他不能開到有車的門
所以在下面兩個可能性中都各別被迫只能用100%的機率開啟2或3號門
這個環節就是造成後面機率分佈開始被打亂的原因 也就是增加了新的"條件"
我加上綠點的地方是最後有選到車的狀況 自己作點基本的計算吧
無題 無名 21/01/14(四)22:11:30 ID:S8iIqmQ6 No.2186317
無題 無名 21/01/14(四)22:41:21 ID:xFbQyGEo No.2186324
>>2186304
這是正確解答
原始機率本來就不會變
早就說過這跟那個3人買東西剩下3元平分的題目一樣
用一點小技巧耍耍文組腦
就讓他們以為錢變少有人偷錢的感覺罷了
充其量就是文組式數學
簡單的講只是文字遊戲
而這種也是很多政客喜歡用來騙選票的大絕招
但可悲的是
絕大部分人看不出問題來
確實會傻傻的被騙去相信
所以很常聽人勸說一句話
「當迷惑混淆的時候去回想最初的原點是什麼」
那也許就是你要的答案
這是正確解答
原始機率本來就不會變
早就說過這跟那個3人買東西剩下3元平分的題目一樣
用一點小技巧耍耍文組腦
就讓他們以為錢變少有人偷錢的感覺罷了
充其量就是文組式數學
簡單的講只是文字遊戲
而這種也是很多政客喜歡用來騙選票的大絕招
但可悲的是
絕大部分人看不出問題來
確實會傻傻的被騙去相信
所以很常聽人勸說一句話
「當迷惑混淆的時候去回想最初的原點是什麼」
那也許就是你要的答案
無題 無名 21/01/14(四)22:41:30 ID:B3ST0zxE No.2186325
>>2186299
那個1/2並不是你說的門後有車的機率
而是來賓選擇換或不換的機率
因為只有換或不換兩種,所以當然是各1/2
至於你說的門後有車的機率
因為條件機率可以用公式表現
P(A|B) = P(A∩B)/P(B)
如果你打算讓大家明白你講的門後有車是什麼意思
你應該指出是P(A|B)、P(A∩B)還是P(B)
那個1/2並不是你說的門後有車的機率
而是來賓選擇換或不換的機率
因為只有換或不換兩種,所以當然是各1/2
至於你說的門後有車的機率
因為條件機率可以用公式表現
P(A|B) = P(A∩B)/P(B)
如果你打算讓大家明白你講的門後有車是什麼意思
你應該指出是P(A|B)、P(A∩B)還是P(B)
無題 無名 21/01/14(四)23:51:44 ID:PxEKtYmk No.2186338
附圖又小修了一下
藍框為中獎的狀況
紅點是不換門
綠點是換門
附圖羅列了一開始選擇1號門之後
"隨機選擇"是否換門的所有可能狀況與機率
可整理出以下資訊
先不管中獎與否 發生"不換門"的機率為
(1/12)+(1/12)+(1/6)+(1/6)=1/2
而在這1/2的狀況當中 中獎即為紅點與藍框的交集處
機率為
(1/12)+(1/12)=1/6
突然發現怎麼又跑出了個1/6???
不用驚慌 因為這是"隨機選擇是否換門的前提下"
同時發生"不換門"與"中獎"這兩件事情的機率
因此我們要將"換門"的決定方式由隨機改為"一定不換門"
(1/6)/(1/2)=1/3 確定不換門下的中獎率1/3就這樣出來了
而堅持換門的機率就是
(1/12)+(1/12)+(1/6)+(1/6)=(1/2)
換門+中獎的發生率為
(1/6)+(1/6)=1/3
確定換門下的中獎率為
(1/3)/(1/2)=2/3
說真的羅列越多數字跟計算過程反而會讓人看著眼花
最好還是看我的附圖跟第一段內容自己仔細思考吧
藍框為中獎的狀況
紅點是不換門
綠點是換門
附圖羅列了一開始選擇1號門之後
"隨機選擇"是否換門的所有可能狀況與機率
可整理出以下資訊
先不管中獎與否 發生"不換門"的機率為
(1/12)+(1/12)+(1/6)+(1/6)=1/2
而在這1/2的狀況當中 中獎即為紅點與藍框的交集處
機率為
(1/12)+(1/12)=1/6
突然發現怎麼又跑出了個1/6???
不用驚慌 因為這是"隨機選擇是否換門的前提下"
同時發生"不換門"與"中獎"這兩件事情的機率
因此我們要將"換門"的決定方式由隨機改為"一定不換門"
(1/6)/(1/2)=1/3 確定不換門下的中獎率1/3就這樣出來了
而堅持換門的機率就是
(1/12)+(1/12)+(1/6)+(1/6)=(1/2)
換門+中獎的發生率為
(1/6)+(1/6)=1/3
確定換門下的中獎率為
(1/3)/(1/2)=2/3
說真的羅列越多數字跟計算過程反而會讓人看著眼花
最好還是看我的附圖跟第一段內容自己仔細思考吧
無題 無名 21/01/15(五)05:19:04 ID:XTqiRzJ2 No.2186367
>>2186304
大致沒錯 但對於看不懂的部分人來說有個問題
那就是為什麼
>第一次選中車 換門=得A/B
得到A跟B是不同的事件怎麼能並在同一條內
如果要解決這問題附圖是"在維持每個事件機率均等"的前提下列出的12種可能性
C欄是"主持人先隨機選擇一扇門"
但又因為規則限制 當選到車的時候必須換成羊
因此就會有紅底的四種狀況 本來選到車門 卻被規則限制改成羊門
D欄就是最後玩家見到主持人開啟的門
F欄綠底是有選到車的狀況
前面E欄的藍底是換門 黃底是不換
從這表格中可以明確地看出換門的中獎率是不換的兩倍
如果把C欄遮住 可以很神奇的發現
5號跟7號
6號跟8號
9號跟11號
10號跟12號
這幾組在事件是一模一樣的 這是由於加入了遊戲規則
導致在玩家眼中各個事件發生的機率不均等的原因
大致沒錯 但對於看不懂的部分人來說有個問題
那就是為什麼
>第一次選中車 換門=得A/B
得到A跟B是不同的事件怎麼能並在同一條內
如果要解決這問題附圖是"在維持每個事件機率均等"的前提下列出的12種可能性
C欄是"主持人先隨機選擇一扇門"
但又因為規則限制 當選到車的時候必須換成羊
因此就會有紅底的四種狀況 本來選到車門 卻被規則限制改成羊門
D欄就是最後玩家見到主持人開啟的門
F欄綠底是有選到車的狀況
前面E欄的藍底是換門 黃底是不換
從這表格中可以明確地看出換門的中獎率是不換的兩倍
如果把C欄遮住 可以很神奇的發現
5號跟7號
6號跟8號
9號跟11號
10號跟12號
這幾組在事件是一模一樣的 這是由於加入了遊戲規則
導致在玩家眼中各個事件發生的機率不均等的原因
無題 無名 21/01/15(五)07:20:29 ID:68hwQaL2 No.2186369
>>2186299
沒想到你這個白癡還是在說1/2阿(笑
沒看到文章都說忽略了前面的條件嗎
有種再開一串讓大家來笑你啊
而且你還是沒解釋不換門有1/3中車,門後有車的機率卻是1/2的情況阿
中車的定義就是門後有車,白癡
沒想到你這個白癡還是在說1/2阿(笑
沒看到文章都說忽略了前面的條件嗎
有種再開一串讓大家來笑你啊
而且你還是沒解釋不換門有1/3中車,門後有車的機率卻是1/2的情況阿
中車的定義就是門後有車,白癡
無題 無名 21/01/15(五)07:22:43 ID:68hwQaL2 No.2186370
想簡單點很容易理解2/3 想得太複雜反而容易中陷阱
無題 無名 21/01/16(六)20:04:06 ID:wHtE9MyY No.2186729