評分:0, 年:0, 月:0, 週:0, 日:0, [+1 / -1] 最後更新:2019-05-12 20:42:37
無本文
無題 無名 19/05/10(五)15:44:07 ID:qT/ygbLQ No.1254852
喔啊,我感覺到了
那種山雨欲來風滿樓的氣氛
那種山雨欲來風滿樓的氣氛
無題 無名 19/05/10(五)16:10:53 ID:GdBBJidw No.1254896
無題 工程統計學上完之後就都還回去了...... 19/05/10(五)16:11:44 ID:zPQ9Pfok No.1254897
>>1254850
so......那個"大獎換不換"選"換"之後中獎的機率到底是多少?有誰可以用土木系也聽得懂的方式解釋一下?
so......那個"大獎換不換"選"換"之後中獎的機率到底是多少?有誰可以用土木系也聽得懂的方式解釋一下?
無題 無名 19/05/10(五)16:17:04 ID:KeVAXbyk No.1254901
>>1254897
https://www.youtube.com/watch?v=eYmSDnVFxT4
https://www.youtube.com/watch?v=eYmSDnVFxT4
所謂的哥布林 其實就是無知嗎???
錯 這個老爸雖然無法理解數學 卻承認有一個答案比他覺得是對的答案更對
真正無知的人 應該會認為跟自己邏輯不同的答案是錯的
也就是說 老爸並不是根據自己的理解來理解數學問題 而是根據權威 要是有權威人士告訴他答案 就算不符合他的邏輯他也相信是對的
是相信自己的邏輯好 還是放棄邏輯相信權威好呢...
錯 這個老爸雖然無法理解數學 卻承認有一個答案比他覺得是對的答案更對
真正無知的人 應該會認為跟自己邏輯不同的答案是錯的
也就是說 老爸並不是根據自己的理解來理解數學問題 而是根據權威 要是有權威人士告訴他答案 就算不符合他的邏輯他也相信是對的
是相信自己的邏輯好 還是放棄邏輯相信權威好呢...
>>1254912
>這個老爸雖然無法理解數學
>卻承認有一個答案比他覺得是對的答案更對
>真正無知的人(ry
但這種思考方式其實已經算是部分踏進陰謀論者的領域裡了耶
「覺得自己的答案才是世間普遍正解」
跟「一定有個超越現在權威人士所說的答案雖然我不知道(也不去求證)」
都很容易被別人靠著話術、魅力所提出的「新答案」呼嚨
>這個老爸雖然無法理解數學
>卻承認有一個答案比他覺得是對的答案更對
>真正無知的人(ry
但這種思考方式其實已經算是部分踏進陰謀論者的領域裡了耶
「覺得自己的答案才是世間普遍正解」
跟「一定有個超越現在權威人士所說的答案雖然我不知道(也不去求證)」
都很容易被別人靠著話術、魅力所提出的「新答案」呼嚨
無題 無名 19/05/10(五)16:41:59 ID:fkEDbahg No.1254923
>>1254923
因為你原本選到羊的機率是2/3,所以在之後重新選擇的時候因為另一隻羊已經被剃除掉了,所以翻轉的結果就是換中汽車的機率變成2/3
因為你原本選到羊的機率是2/3,所以在之後重新選擇的時候因為另一隻羊已經被剃除掉了,所以翻轉的結果就是換中汽車的機率變成2/3
無題 無名 19/05/10(五)16:47:09 ID:rU/thWGQ No.1254931
>>1254923
因為你選中A和選中C的機率不一樣
因為你選中A和選中C的機率不一樣
無題 無名 19/05/10(五)16:48:19 ID:AAKuT0Po No.1254932
沒選的2扇打開有羊的那一扇這其實是甚麼意思
如果沒選的2扇都有羊該怎麼辦?
假設羊X2也只開一扇
先選中大獎是1/3, 如果換的話是100%羊
先選中羊是2/3, 換的話是各50%
所以換的期待值1/3*1*0+2/3*0.5*1+2/3*0.5*0=1/3
沒變吧
大學不是理科求指教
如果沒選的2扇都有羊該怎麼辦?
假設羊X2也只開一扇
先選中大獎是1/3, 如果換的話是100%羊
先選中羊是2/3, 換的話是各50%
所以換的期待值1/3*1*0+2/3*0.5*1+2/3*0.5*0=1/3
沒變吧
大學不是理科求指教
>>1254923
如果遊戲一開始就讓你選2扇門你的中獎機率是不是2/3
對吧?
你一開始從3門中選了A,中獎率1/3,最後堅決不換,中獎率還是1/3
到這裡可以理解吧?
你一開始選了A,主持人開了B,你決定改C,這裡先暫停
回到遊戲一開始,你是不是相當於一次選了B跟C
所以決定換的話你的中獎率是不是2/3
明白了嗎?
我也土木系的,我都懂了你也可以的
如果遊戲一開始就讓你選2扇門你的中獎機率是不是2/3
對吧?
你一開始從3門中選了A,中獎率1/3,最後堅決不換,中獎率還是1/3
到這裡可以理解吧?
你一開始選了A,主持人開了B,你決定改C,這裡先暫停
回到遊戲一開始,你是不是相當於一次選了B跟C
所以決定換的話你的中獎率是不是2/3
明白了嗎?
我也土木系的,我都懂了你也可以的
無題 無名 19/05/10(五)16:51:36 ID:o5bFd7sE No.1254937
>>1254933
看來上面的回覆只能說機率數學有夠可惡
看來上面的回覆只能說機率數學有夠可惡
>>1254923
因為不是單看當下的兩個門
你一開始選擇一個門,即使沒打開但這已經是一個選擇動作
你選中的機率是1/3,沒中是2/3
然後把一扇門去掉,那扇門是沒中的
如果你不換,直接開你第一次選的門,你還是跟第一次一樣1/3
後來去掉門的動作不會影響你第一次選擇的機率
因為那時還是有三個門
如果你換了,那中獎率是 1-(沒中機率1/3) =2/3
用比較不反直覺的誇張範例
一開始有100個門,你選一個,然後主持人去掉了98扇沒中的門
你要不要換?
因為不是單看當下的兩個門
你一開始選擇一個門,即使沒打開但這已經是一個選擇動作
你選中的機率是1/3,沒中是2/3
然後把一扇門去掉,那扇門是沒中的
如果你不換,直接開你第一次選的門,你還是跟第一次一樣1/3
後來去掉門的動作不會影響你第一次選擇的機率
因為那時還是有三個門
如果你換了,那中獎率是 1-(沒中機率1/3) =2/3
用比較不反直覺的誇張範例
一開始有100個門,你選一個,然後主持人去掉了98扇沒中的門
你要不要換?
無題 無名 19/05/10(五)16:53:34 ID:02E.LOEE No.1254942
>>1254916
所以怎樣才是恰當的思考方式
舉個例子
我應如何說服一個對疫苗稍有懷疑的人呢?
一般人是無法以重現方式驗證對疫苗的指控
但相信權威亦可能是一種盲信
若果說直接去唸書還是唯一正解
這是不是說一般民眾都唸生物或醫學直到他們有能力自行驗證呢?
所以怎樣才是恰當的思考方式
舉個例子
我應如何說服一個對疫苗稍有懷疑的人呢?
一般人是無法以重現方式驗證對疫苗的指控
但相信權威亦可能是一種盲信
若果說直接去唸書還是唯一正解
這是不是說一般民眾都唸生物或醫學直到他們有能力自行驗證呢?
無題 無名 19/05/10(五)16:59:58 ID:2bHmostQ No.1254951
>>1254936
不不不,土木系的是我不是他別亂冤枉人啊www
會提問的原因是因為當初上課的時候老師是直接模擬讓我們了解機率何在,
結果抓出來示範的三個人就是這麼賽都第一個選到大獎那一邊WWW
然後唯一一個打死也不換的就這麼成為該堂課唯一得到獎品的,
導致我到現在對這個機率問題都還有點錯誤認知w
不不不,土木系的是我不是他別亂冤枉人啊www
會提問的原因是因為當初上課的時候老師是直接模擬讓我們了解機率何在,
結果抓出來示範的三個人就是這麼賽都第一個選到大獎那一邊WWW
然後唯一一個打死也不換的就這麼成為該堂課唯一得到獎品的,
導致我到現在對這個機率問題都還有點錯誤認知w
無題 無名 19/05/10(五)17:01:01 ID:nBCF9Kps No.1254953
又要來一次嗎?
選項ABC,命中率平均都是1/3
假設選了A,然後別人開了B沒中問你要不要轉為C
轉的話等同同時選了BC所以是1/3+1/3=2/3,或換個說法你放棄了原有的1/3然後你也沒其他能選所以是2/3
不轉還是保持1/3
當然你是ATM的話就算是1億選1還是神抽
選項ABC,命中率平均都是1/3
假設選了A,然後別人開了B沒中問你要不要轉為C
轉的話等同同時選了BC所以是1/3+1/3=2/3,或換個說法你放棄了原有的1/3然後你也沒其他能選所以是2/3
不轉還是保持1/3
當然你是ATM的話就算是1億選1還是神抽
無題 無名 19/05/10(五)17:01:20 ID:Ifz4l.W2 No.1254954
>>1254949
呃⋯⋯讓他們自然病死好讓「因為白癡理由而堅持己見」的基因消失?
呃⋯⋯讓他們自然病死好讓「因為白癡理由而堅持己見」的基因消失?
無題 無名 19/05/10(五)17:02:09 ID:FzWcERj. No.1254955
無題 無名 19/05/10(五)17:02:49 ID:2bHmostQ No.1254956
最大難關應該是不換門跟換門都是二選一
很難理解換門會有較高機率中獎
很難理解換門會有較高機率中獎
無題 無名 19/05/10(五)17:08:11 ID:fkEDbahg No.1254962
無題 無名 19/05/10(五)17:08:13 ID:qfadDXvs No.1254963
無題 無名 19/05/10(五)17:10:15 ID:2bHmostQ No.1254966
無題 無名 19/05/10(五)17:13:16 ID:b06yptcM No.1254971
>>1254957
樣本數極低的情況機率當然沒卵用
樣本數極低的情況機率當然沒卵用
無題 無名 19/05/10(五)17:39:19 ID:OIVaiyDg No.1254993
無題 無名 19/05/10(五)17:40:42 ID:2FbWsP/c No.1254995
整串看下來
我面前漸漸浮現出大二機率老師的臉
我面前漸漸浮現出大二機率老師的臉
無題 無名 19/05/10(五)17:45:08 ID:nBCF9Kps No.1254998
>>1254993
出現了,是邏輯智障
出現了,是邏輯智障
無題 無名 19/05/10(五)17:46:30 ID:aOiM0rCs No.1254999
整串看下來
我面前漸漸浮現出凱文史貝西的臉
我面前漸漸浮現出凱文史貝西的臉
無題 無名 19/05/10(五)17:51:57 ID:eCfNfJEI No.1255002
無題 無名 19/05/10(五)17:53:05 ID:CA1Xm.PI No.1255005
無題 無名 19/05/10(五)18:00:42 ID:LxKMcaoA No.1255010
無題 無名 19/05/10(五)18:03:35 ID:fypSisEw No.1255013
無題 無名 19/05/10(五)18:14:39 ID:vDMmxALQ No.1255021
>>1254993
恩你說的對
恩你說的對
無題 無名 19/05/10(五)18:24:55 ID:qKghcwAY No.1255027
無題 無名 19/05/10(五)18:28:59 ID:to6iRCYw No.1255028
>>1254949
其實我打疫苗也只是相信權威而已啊...我真的不覺得自己有多理性 也沒很懂啊 身邊的人都笑陰謀論 我也跟著笑
我不想扯太多陰謀論 只想要講所謂科普這種中國提出的理想
科普的人真的覺得 每個人都該去讀生物跟醫學 對他們來說讀到略懂疫苗原理 也不過是高中必修的程度而已 他們還覺得科學的態度就是懷疑 常識隨時被推翻 他們覺得很快樂
或者有的重視實用的人就會說 科普到可以擊退陰謀論和迷信的程度就好 剩下的有需要再學
其實我打疫苗也只是相信權威而已啊...我真的不覺得自己有多理性 也沒很懂啊 身邊的人都笑陰謀論 我也跟著笑
我不想扯太多陰謀論 只想要講所謂科普這種中國提出的理想
科普的人真的覺得 每個人都該去讀生物跟醫學 對他們來說讀到略懂疫苗原理 也不過是高中必修的程度而已 他們還覺得科學的態度就是懷疑 常識隨時被推翻 他們覺得很快樂
或者有的重視實用的人就會說 科普到可以擊退陰謀論和迷信的程度就好 剩下的有需要再學
無題 無名 19/05/10(五)18:35:54 ID:4BO.DVuw No.1255033
>>1254993
因為你把前提「已知打開的一道門是沒有」這點忽略
因為你把前提「已知打開的一道門是沒有」這點忽略
無題 無名 19/05/10(五)18:36:42 ID:/3eKCvoI No.1255035
換個數字想
今天有100個門99個垃圾、1個大獎
主持人幫你開了80扇門
這樣就比較好理解了
今天有100個門99個垃圾、1個大獎
主持人幫你開了80扇門
這樣就比較好理解了
無題 無名 19/05/10(五)18:40:46 ID:2R2ZAaWI No.1255036
>>1255040
可是主持人自己先把門打開讓我知道三扇門中其中一個是羊,也就是只剩下兩個未知之門,主持人還願意讓我更換門的情況,此時中獎率不是該變成1/2嗎?
因為有一個門已經先被排除了,我絕對不可能去選。那就只剩下我剛才選的門+沒有被公布答案的門。
可是主持人自己先把門打開讓我知道三扇門中其中一個是羊,也就是只剩下兩個未知之門,主持人還願意讓我更換門的情況,此時中獎率不是該變成1/2嗎?
因為有一個門已經先被排除了,我絕對不可能去選。那就只剩下我剛才選的門+沒有被公布答案的門。
無題 無名 19/05/10(五)18:59:33 ID:TlApILtw No.1255050
重點在於一句題目中沒說到的話
「主持人絕對不會很雞掰的打開那個有大奬的門」
這代表他砍了一個選項後,大奬一定還留在其中,就是這個刻意的「人擇」讓更換的機率自50%提高到66%
「主持人絕對不會很雞掰的打開那個有大奬的門」
這代表他砍了一個選項後,大奬一定還留在其中,就是這個刻意的「人擇」讓更換的機率自50%提高到66%
無題 無名 19/05/10(五)18:59:46 ID:1H/XbgvY No.1255053
>>1254993
你一開始就選中的話剩下兩扇門都是沒中的 不管去掉哪扇剩的都是沒中的 所以換了之後一定不中
你一開始沒選中的話剩下有中沒中各一扇 去掉沒中那扇後只剩中獎的 所以換了之後一定會中
也就是說
不換的話你必須一開始就選到對的三分之一才能中獎
但換了的話如果你一開始選到錯的三分之二都能中獎
你一開始就選中的話剩下兩扇門都是沒中的 不管去掉哪扇剩的都是沒中的 所以換了之後一定不中
你一開始沒選中的話剩下有中沒中各一扇 去掉沒中那扇後只剩中獎的 所以換了之後一定會中
也就是說
不換的話你必須一開始就選到對的三分之一才能中獎
但換了的話如果你一開始選到錯的三分之二都能中獎
無題 無名 19/05/10(五)19:00:06 ID:fkEDbahg No.1255055
理論就是理論,數據就是數據
但現實就是現實
換門了,理論上就是2/3會中獎,但實際上,你不能掌控那餘下的1/3去嘔心你
只要結果一天不出,機率永遠只是機率,數據永遠只是數據
但現實就是現實
換門了,理論上就是2/3會中獎,但實際上,你不能掌控那餘下的1/3去嘔心你
只要結果一天不出,機率永遠只是機率,數據永遠只是數據
有人說把所有可能列出來,
A是獎品BC是其他()是選擇的,首輪是
(A)BC A(B)C AB(C)
因為主持人排除一個不中的,那剩下的組合是
(A)B (A)C A(B) A(C)
此時不換組合是
(A) (A) (B) (C)
如果換,組合是
(B) (C) (A) (A)
換不換都是50%選A啊島民可以解說嗎?
A是獎品BC是其他()是選擇的,首輪是
(A)BC A(B)C AB(C)
因為主持人排除一個不中的,那剩下的組合是
(A)B (A)C A(B) A(C)
此時不換組合是
(A) (A) (B) (C)
如果換,組合是
(B) (C) (A) (A)
換不換都是50%選A啊島民可以解說嗎?
無題 無名 19/05/10(五)19:04:30 ID:rU/thWGQ No.1255058
>>1255045
剩下的兩個門並不是讓你抽選
而是讓你決定要不要更換剛剛的答案
因此你剛剛選了什麼的機率就很重要
如果今天不是典型的蒙提霍爾問題
改成袋子裡有三顆球,先讓你抽一顆但不能看抽到的結果
然後用黑科技把沒中的球排除,再讓你重新取球的話
這種情況就會是1/2
因為你剛剛抽到什麼一點也不影響下次的抽選
剩下的兩個門並不是讓你抽選
而是讓你決定要不要更換剛剛的答案
因此你剛剛選了什麼的機率就很重要
如果今天不是典型的蒙提霍爾問題
改成袋子裡有三顆球,先讓你抽一顆但不能看抽到的結果
然後用黑科技把沒中的球排除,再讓你重新取球的話
這種情況就會是1/2
因為你剛剛抽到什麼一點也不影響下次的抽選
中獎,幹!這機率不是超高的嗎 (2/3)
沒中,幹!狗屎爛機率 (2/3)
討論機率時請停止你的人類情緒,幸運是個人固有技能,不能帶入計算
沒中,幹!狗屎爛機率 (2/3)
討論機率時請停止你的人類情緒,幸運是個人固有技能,不能帶入計算
>>1255045
重點是你在「還有三扇門」的時候就選了 所以你手上那扇門的中獎率就是三分之一
今天假設是一萬扇門 你選了之後的槓龜率就是9999/10000
就算主持弄掉9998扇沒中的門 一樣不改你選擇手上那扇門時的槓龜率
重點是你在「還有三扇門」的時候就選了 所以你手上那扇門的中獎率就是三分之一
今天假設是一萬扇門 你選了之後的槓龜率就是9999/10000
就算主持弄掉9998扇沒中的門 一樣不改你選擇手上那扇門時的槓龜率
無題 無名 19/05/10(五)19:11:24 ID:0CBm15n2 No.1255068
有1/3會贏,2/3會輸
1/3贏的世界線若選換則會輸 -> 也就是如果換,輸的機率是1/3
1/3贏的世界線若選換則會輸 -> 也就是如果換,輸的機率是1/3
無題 無名 19/05/10(五)19:15:43 ID:fkEDbahg No.1255076
>>1255056
(A)B (A)C A(B) A(C)
這四個的發生率不同
(A)B (A)C是同樣因為(A)BC而產生的,加起來只占1/3
A(B) A(C)則是各占了1/3,因為他們的上游選項都不會衍生出其他可能
所以你到底要不要回去國中重讀
(A)B (A)C A(B) A(C)
這四個的發生率不同
(A)B (A)C是同樣因為(A)BC而產生的,加起來只占1/3
A(B) A(C)則是各占了1/3,因為他們的上游選項都不會衍生出其他可能
所以你到底要不要回去國中重讀
>>1255066
所以學邏輯和解讀機率也並不能改變未來/真實,只是會讓自己贏/輸得合理一點
所以學邏輯和解讀機率也並不能改變未來/真實,只是會讓自己贏/輸得合理一點
無題 無名 19/05/10(五)19:20:22 ID:yXxJYq1I No.1255083
有人說了,一條重要規則是主持人不會去開有獎的門,所以
你自己選,你有1/3的機會選中獎
主持人開門之後還是堅持,那就跟上面一樣,你有1/3的機會選中獎
你乖乖換,你會輸掉的情況只有一種,你一開始就選到中獎那個,所以你有1/3的機率輸掉,也就是2/3的勝率
你自己選,你有1/3的機會選中獎
主持人開門之後還是堅持,那就跟上面一樣,你有1/3的機會選中獎
你乖乖換,你會輸掉的情況只有一種,你一開始就選到中獎那個,所以你有1/3的機率輸掉,也就是2/3的勝率
無題 無名 19/05/10(五)19:34:39 ID:AaWH7gfU No.1255102
無題 無名 19/05/10(五)19:47:30 ID:AAKuT0Po No.1255114
>>1255106
的確...但就如NGNL所說的,不是思考1/2或者2/3,而是思考怎變成100%
這樣錢才一定不會變成灰
用回遊戲,其實還要思考主持人其實有沒有可能可以隨意改答案之類的
如果可以,那你抽中車的機率從一開始就是0或者100
用錢先收買主持人也是個方法
的確...但就如NGNL所說的,不是思考1/2或者2/3,而是思考怎變成100%
這樣錢才一定不會變成灰
用回遊戲,其實還要思考主持人其實有沒有可能可以隨意改答案之類的
如果可以,那你抽中車的機率從一開始就是0或者100
用錢先收買主持人也是個方法
無題 無名 19/05/10(五)19:55:53 ID:f6N5dKSU No.1255123
>>1254989
賭場還外加上限問題
賭場還外加上限問題
無題 無名 19/05/10(五)19:55:53 ID:f6N5dKSU No.1255124
>>1254989
賭場還外加上限問題
賭場還外加上限問題
無題 無名 19/05/10(五)19:56:36 ID:MBWFhspw No.1255126
>>1255093
精闢的解釋
精闢的解釋
無題 無名 19/05/10(五)22:25:25 ID:2R2ZAaWI No.1255283
那麼那個24人裡有兩個人生日可能會一樣是怎麼算的啊?
無題 無名 19/05/10(五)22:27:44 ID:cCAkiPAk No.1255285
>>1255283
https://zh.wikipedia.org/wiki/%E7%94%9F%E6%97%A5%E5%95%8F%E9%A1%8C
https://zh.wikipedia.org/wiki/%E7%94%9F%E6%97%A5%E5%95%8F%E9%A1%8C
無題 無名 19/05/10(五)22:29:17 ID:yjnBDgxk No.1255289
>>1255283
https://zh.wikipedia.org/wiki/%E7%94%9F%E6%97%A5%E5%95%8F%E9%A1%8C
https://zh.wikipedia.org/wiki/%E7%94%9F%E6%97%A5%E5%95%8F%E9%A1%8C
雖然你們說的都很有道理...可是為什麼人的想法跟邏輯比起來就是差那麼多呢....我開始相信這個老爸說的哥布林的惡意了
無題 無名 19/05/10(五)22:30:05 ID:qz2otiUI No.1255292
無題 無名 19/05/10(五)22:37:07 ID:4BO.DVuw No.1255309
>>1255291
因為人會受日常常識和直覺左右思考
因為人會受日常常識和直覺左右思考
無題 無名 19/05/10(五)22:40:54 ID:o3ZUgtTM No.1255315
無題 無名 19/05/10(五)22:43:21 ID:CqHAzUFU No.1255322
我想到一個絕妙的證明天天都生日
可惜這裡的串保存不久無法一一寫下
可惜這裡的串保存不久無法一一寫下
無題 無名 19/05/10(五)22:52:58 ID:21lUBUYM No.1255335
無題 無名 19/05/10(五)22:57:04 ID:qz2otiUI No.1255339
流言終結者2011年 第九季18集 全部集數第177
Wheel of MythFortune
標題 Wheel of Mythfortune 答覆幸運觀眾
有蒙提霍爾問題
Wheel of MythFortune
標題 Wheel of Mythfortune 答覆幸運觀眾
有蒙提霍爾問題
數學哥布林: 1 + 2 + 3 + ... + 到無限 = -1/12
無題 無名 19/05/11(六)04:38:21 ID:NcklVB1M No.1255549
>>1255419
https://www.youtube.com/watch?v=YuIIjLr6vUA
https://www.youtube.com/watch?v=YuIIjLr6vUA
無題 無名 19/05/11(六)06:08:41 ID:hVa069q. No.1255564
無題 無名 19/05/11(六)06:09:41 ID:.U0ky82. No.1255565
肥宅課金抽卡的時候有這麼理智就好了
無題 無名 19/05/11(六)06:23:50 ID:gVAQOz3E No.1255567
不論我選擇的這扇門打開後是羊或者箱子,只要主持人身後那最後的門還關著,我就能確信自己中獎
無題 無名 19/05/11(六)06:41:42 ID:2GA8fE1M No.1255569
>>1255291
答案是 真正被哥布林搞爛的是人類的直覺
答案是 真正被哥布林搞爛的是人類的直覺
無題 無名 19/05/11(六)06:55:35 ID:2GA8fE1M No.1255574
>>1255082
>所以學邏輯和解讀機率也並不能改變未來/真實,只是會讓自己贏/輸得合理一點
你在說什麼 學邏輯絕對會提高你的勝率 讓你贏 改變未來 改變你的人生啊
定義清楚一點 學了不會改變你第一次盲選三選一的機率 但是可以改變你第二次選的選擇 你的命運真的掌握在你的手裡 你也不需要捨棄人類的情緒 你只要客服衝動 讓情緒臣服於理性的選擇 就可以幸福了 我們每個人都(ry
>所以學邏輯和解讀機率也並不能改變未來/真實,只是會讓自己贏/輸得合理一點
你在說什麼 學邏輯絕對會提高你的勝率 讓你贏 改變未來 改變你的人生啊
定義清楚一點 學了不會改變你第一次盲選三選一的機率 但是可以改變你第二次選的選擇 你的命運真的掌握在你的手裡 你也不需要捨棄人類的情緒 你只要客服衝動 讓情緒臣服於理性的選擇 就可以幸福了 我們每個人都(ry
聽過最簡單的解釋
假如有100扇門,你選1扇後,主持人會把98扇拿走,餘下1扇問你換不換
那麼,一開始就選中的機率是1/100
換的話就是99/100
同理代入3扇門,就是1/3和2/3
這樣你可以明白了吧
假如有100扇門,你選1扇後,主持人會把98扇拿走,餘下1扇問你換不換
那麼,一開始就選中的機率是1/100
換的話就是99/100
同理代入3扇門,就是1/3和2/3
這樣你可以明白了吧
無題 無名 19/05/11(六)11:05:26 ID:dYBDk8uE No.1255680
>>1255410
然後他們實際實驗出來的結果
(分兩組,每組隨機100次抽門,一組決不換門,一組絕對換門....而且不是電腦模擬,是真人手動選擇哪扇門)
結果是換門贏的機率真的是不換的兩倍
(實際的數學原理搞不懂沒關係,只要記得實際抽牌的結果就是換比不換還要好就行了)
然後他們實際實驗出來的結果
(分兩組,每組隨機100次抽門,一組決不換門,一組絕對換門....而且不是電腦模擬,是真人手動選擇哪扇門)
結果是換門贏的機率真的是不換的兩倍
(實際的數學原理搞不懂沒關係,只要記得實際抽牌的結果就是換比不換還要好就行了)
條件改變後就不能用原本的1/3去看吧?
難道選擇題第一題是四選一答案是A,下一題的三選一你猜中答案的機率會被影響?
難道選擇題第一題是四選一答案是A,下一題的三選一你猜中答案的機率會被影響?
無題 無名 19/05/11(六)11:54:09 ID:3PuYT2v2 No.1255724
>>1254993
你的人生真的很快樂 所有的機率在你的邏輯下就會只剩下中和不中有和沒有 而忽略其他的要素....讚!
你的人生真的很快樂 所有的機率在你的邏輯下就會只剩下中和不中有和沒有 而忽略其他的要素....讚!
無題 無名 19/05/11(六)11:56:49 ID:aUMVxr1s No.1255728
無題 無名 19/05/11(六)12:07:02 ID:OJM93ojA No.1255740
>>1255651
用高機率刷掉一開始就選中的可能性
用數學去解釋你這個選擇是1/100
剩下另一個選擇已經不是1/2, 而是99/100
一切都是反選
'你一開始選的那個很大機會不是喔,剩下那個你想想還可能會比你現在選的機會更低嗎?還不轉!!!'
用高機率刷掉一開始就選中的可能性
用數學去解釋你這個選擇是1/100
剩下另一個選擇已經不是1/2, 而是99/100
一切都是反選
'你一開始選的那個很大機會不是喔,剩下那個你想想還可能會比你現在選的機會更低嗎?還不轉!!!'
無題 無名 19/05/11(六)12:08:59 ID:PPcqbYqE No.1255742
>>1255706
因為你是在一開始就做了選擇,所以條件並沒有改變。
因為你是在一開始就做了選擇,所以條件並沒有改變。
我覺得這一串有很多數學哥布林
>>1255854
可是哥殺不是有出現了怎麼還會有哥布林?.....
可是哥殺不是有出現了怎麼還會有哥布林?.....
無題 無名 19/05/11(六)14:28:08 ID:f5hutMCc No.1255863
>>1255861別忘記神手一揮就會有一窩哥布林出現
無題 無名 19/05/11(六)14:32:05 ID:Jf8OcU3E No.1255867
>>1255861
數學哥殺把數學哥布林殺光了
所以才一堆人搞錯了
但上面有人說那是「直覺」是不對的
例如換門,那是由於小時候學過的算數使我們認為機會率一樣
0.999...也一樣,循環小數、無限小之類的概念不是能直覺得來
數學哥殺把數學哥布林殺光了
所以才一堆人搞錯了
但上面有人說那是「直覺」是不對的
例如換門,那是由於小時候學過的算數使我們認為機會率一樣
0.999...也一樣,循環小數、無限小之類的概念不是能直覺得來
無題 無名 19/05/11(六)14:54:54 ID:2Modn6g6 No.1255880
真正的哥布林
就是當你換門後,勝率變成2/3或者98/100時
就偷偷把大獎放在你原本的門內...
就是當你換門後,勝率變成2/3或者98/100時
就偷偷把大獎放在你原本的門內...
>>1255885
由於每一次抽獎機率都是獨立的
所以你這次抽獎沒中並不會增加下次抽獎抽中的機率喔
連續抽一百次:中獎率為 63.4%
連續抽兩百次:中獎率為 86.7%
連續抽三百次:中獎率為 95.1%
不用謝,祝抽獎愉快!
由於每一次抽獎機率都是獨立的
所以你這次抽獎沒中並不會增加下次抽獎抽中的機率喔
連續抽一百次:中獎率為 63.4%
連續抽兩百次:中獎率為 86.7%
連續抽三百次:中獎率為 95.1%
不用謝,祝抽獎愉快!
>>1255885
手遊抽角色卡池並不會因為你抽了而機率上產生任何改變,因為是卡牌數量並沒有"減少"的概念.
假設卡池1000張裡只有10張SSR,
第一次十抽後卡池中卡的數量並不會變成990,還是1000,
第二次十抽後卡池內還是1000(以下略
所以無論你幾百幾千幾萬抽機率都一樣,除非該遊戲是設計成有保底機制.
結論: 沒保底情況下機率根本就安慰劑而已,毫無卵用
手遊抽角色卡池並不會因為你抽了而機率上產生任何改變,因為是卡牌數量並沒有"減少"的概念.
假設卡池1000張裡只有10張SSR,
第一次十抽後卡池中卡的數量並不會變成990,還是1000,
第二次十抽後卡池內還是1000(以下略
所以無論你幾百幾千幾萬抽機率都一樣,除非該遊戲是設計成有保底機制.
結論: 沒保底情況下機率根本就安慰劑而已,毫無卵用
無題 無名 19/05/11(六)15:56:29 ID:vAZERUhE No.1255926
>>1255936
剛好相反,其實直覺是反而是最準確的模式,因為人的直覺是腦部計算後的結果,但人往往無法理解直覺的計算,所以得出這樣的結論
https://www.bbc.com/ukchina/trad/amp/vert-fut-44562249
剛好相反,其實直覺是反而是最準確的模式,因為人的直覺是腦部計算後的結果,但人往往無法理解直覺的計算,所以得出這樣的結論
https://www.bbc.com/ukchina/trad/amp/vert-fut-44562249
無題 無名 19/05/11(六)20:31:35 ID:Jf8OcU3E No.1256166
>>1256184
那無限長數列怎麼可以任意使用有限長的計算方式處理?
那無限長數列怎麼可以任意使用有限長的計算方式處理?
無題 無名 19/05/11(六)21:21:37 ID:9LuWNwRc No.1256193
>>1256105
直覺來自演化
演化這東西只在大多數情況下差不多準
本來就不保證能順利處理細節
如果你的理性完全搞不懂發生了什麼,信直覺通常會比信路人好一點
但如果你有著足以理解事情經過的理性,理性還是比直覺準
直覺來自演化
演化這東西只在大多數情況下差不多準
本來就不保證能順利處理細節
如果你的理性完全搞不懂發生了什麼,信直覺通常會比信路人好一點
但如果你有著足以理解事情經過的理性,理性還是比直覺準
無題 無名 19/05/11(六)21:24:21 ID:HpTpyVt2 No.1256195
>>1256188
所以令人的想法跟邏輯比起來會差那麼多,不會是因為人類的直覺是愚蠢的,而是那些人認知資訊全錯,引致直覺的結果和其他人用公式計算得出來的結果差這麼多
所以令人的想法跟邏輯比起來會差那麼多,不會是因為人類的直覺是愚蠢的,而是那些人認知資訊全錯,引致直覺的結果和其他人用公式計算得出來的結果差這麼多
無題 無名 19/05/11(六)21:24:54 ID:wu3hl9cY No.1256199
無題 無名 19/05/11(六)21:42:34 ID:9oM2ncR6 No.1256225
無題 無名 19/05/11(六)21:49:58 ID:C1jaIP2w No.1256235
>>1256218
並沒有誤差,因為這個悖論早就被現實破解了,
看似與目標的差距永遠會有剩餘距離的1/2。
但實際上肯定會在一定的秒數上被追上。
當時提出悖論的人只不過還沒找到漂亮的解釋,
而這個悖論早就被後世的數學家解釋清楚了。
並沒有誤差,因為這個悖論早就被現實破解了,
看似與目標的差距永遠會有剩餘距離的1/2。
但實際上肯定會在一定的秒數上被追上。
當時提出悖論的人只不過還沒找到漂亮的解釋,
而這個悖論早就被後世的數學家解釋清楚了。
無題 無名 19/05/11(六)21:54:51 ID:KfOK72Pk No.1256242
>>1256265
可是我覺得極限不能畫等號耶,只能算無限逼近
可是我覺得極限不能畫等號耶,只能算無限逼近
>>1256270
這是符號上會讓人誤解的地方
實際上0.9...的真正含意是
lim{n->∞} Σ{i=0~n}0.9*10^(-n)
你只看後半的話的確不會是等號
但是因為有取極限,所以整個式子代表的是到不了的的那個點,也就是1
或者就像剛才說了
因為是無限所以是等號
只要不等於就代表你還沒到無限
這是符號上會讓人誤解的地方
實際上0.9...的真正含意是
lim{n->∞} Σ{i=0~n}0.9*10^(-n)
你只看後半的話的確不會是等號
但是因為有取極限,所以整個式子代表的是到不了的的那個點,也就是1
或者就像剛才說了
因為是無限所以是等號
只要不等於就代表你還沒到無限
無題 無名 19/05/11(六)22:25:24 ID:WVzkv5KM No.1256293
>>1256270
>任何一個學生,只要把0.999…設想為一個有限的、不確定的數串,與1的差是無窮小,那麼他就「還沒有對無限小數形成一個完整的過程概念」。其他對0.999…有了完整的過程概念的學生,仍不一定能把這個過程「概括」成一個「對象概念」,就像他們對1的對象概念那樣,所以仍然覺得0.999…和1是不一致的。
>任何一個學生,只要把0.999…設想為一個有限的、不確定的數串,與1的差是無窮小,那麼他就「還沒有對無限小數形成一個完整的過程概念」。其他對0.999…有了完整的過程概念的學生,仍不一定能把這個過程「概括」成一個「對象概念」,就像他們對1的對象概念那樣,所以仍然覺得0.999…和1是不一致的。
>>1256290
所以0.999999...代表的是無線數列的極限值
所以0.99999...與一丸全相等是一個帶有誤導人的敘述。
正確來說應該是0.99999.....的極限值等於1。
至於0.99999...本身是否與1相等則不是該敘述表達的。
所以0.999999...代表的是無線數列的極限值
所以0.99999...與一丸全相等是一個帶有誤導人的敘述。
正確來說應該是0.99999.....的極限值等於1。
至於0.99999...本身是否與1相等則不是該敘述表達的。
無題 無名 19/05/11(六)22:53:08 ID:Sv15u1.g No.1256337
>>1256319
沒學過latex(死
沒學過latex(死
無題 無名 19/05/11(六)22:57:54 ID:vynmjZzs No.1256340
0.999999....
是否等於一是要看這數值是代表什麼
像是你該吃幾個蘋果,算到最後是這數值你就直接吃一個
但如果是要證明啥數值定理還是啥微積分或量子啥的,那就要再評估了
不過基本上對一般人而言是可以直接當成一
是否等於一是要看這數值是代表什麼
像是你該吃幾個蘋果,算到最後是這數值你就直接吃一個
但如果是要證明啥數值定理還是啥微積分或量子啥的,那就要再評估了
不過基本上對一般人而言是可以直接當成一
這裡說的直覺並沒定義
有的人說的天才的直覺 是說遇到問題可以在還沒說明過程就看出答案 我覺得這裡隱含的定義是 對的才叫直覺 你們也可以反對我
可是好笑的是 像這個老爸的表現 他有明白定義 錯了而且無法理解自己為什麼錯才叫"明顯的答案"
這應該很明顯跟天才的直覺是完全不同的東西...應該是腦子轉不過來了...
有的人說的天才的直覺 是說遇到問題可以在還沒說明過程就看出答案 我覺得這裡隱含的定義是 對的才叫直覺 你們也可以反對我
可是好笑的是 像這個老爸的表現 他有明白定義 錯了而且無法理解自己為什麼錯才叫"明顯的答案"
這應該很明顯跟天才的直覺是完全不同的東西...應該是腦子轉不過來了...
無題 無名 19/05/11(六)23:18:13 ID:P3ACM5Rk No.1256361
>>1256342
我認為所謂的「直覺」只是在腦中第一時間出現的答案
而這個「直覺」的出現是大腦根據日常生活的經驗 整理出來的
0.999....=1 的情況中,會覺得違反「直覺」是因為我們在日常生活的數字都是有限數字的
價格會是9.99 之類 因此「直覺」會認為0.99....是有盡頭的
我認為所謂的「直覺」只是在腦中第一時間出現的答案
而這個「直覺」的出現是大腦根據日常生活的經驗 整理出來的
0.999....=1 的情況中,會覺得違反「直覺」是因為我們在日常生活的數字都是有限數字的
價格會是9.99 之類 因此「直覺」會認為0.99....是有盡頭的
希望有弄出來latex(?
$$\lim_{n\rightarrow\infty}\sum_{0}^{n}0.9*10^{-n}$$
總之,基本上
0.9...=$$\lim_{n\rightarrow\infty}\sum_{0}^{n}0.9*10^{-n}$$=1
不認為0.9...等於1的人
要嘛認為$$\lim_{n\rightarrow\infty}\sum_{0}^{n}0.9*10^{-n}$$=1有問題(單純計算問題)
不然就是認為0.9...不是$$\lim_{n\rightarrow\infty}\sum_{0}^{n}0.9*10^{-n}$$
這就是定義問題了,你不接受那就沒辦法,那就叫做你家的數學跟別人不一樣
$$\lim_{n\rightarrow\infty}\sum_{0}^{n}0.9*10^{-n}$$
總之,基本上
0.9...=$$\lim_{n\rightarrow\infty}\sum_{0}^{n}0.9*10^{-n}$$=1
不認為0.9...等於1的人
要嘛認為$$\lim_{n\rightarrow\infty}\sum_{0}^{n}0.9*10^{-n}$$=1有問題(單純計算問題)
不然就是認為0.9...不是$$\lim_{n\rightarrow\infty}\sum_{0}^{n}0.9*10^{-n}$$
這就是定義問題了,你不接受那就沒辦法,那就叫做你家的數學跟別人不一樣
主持人問你要不要換的時候
不是就在2選一嗎
所以為什麼不是50%
不是就在2選一嗎
所以為什麼不是50%
無題 無名 19/05/12(日)00:18:25 ID:FmReo85s No.1256409
無題 無名 19/05/12(日)00:30:28 ID:frOVraYw No.1256416
>>1256403
你只要記得你一開始是在中獎率三分之一狀況下做決定就好了
你只要記得你一開始是在中獎率三分之一狀況下做決定就好了
無題 無名 19/05/12(日)00:32:11 ID:zEOZafis No.1256417
>>1256413
這就普通的1/2啊
這就普通的1/2啊
無題 無名 19/05/12(日)00:32:53 ID:GhgAU3F2 No.1256418
>>1256413
50%
50%
>>1256398
簡單來說,0.9....
可以代換成0.9乘以各次方1/10的數列之和
如此一來就變成一個無窮等比數列,而代入無窮等比數列的和公式去算會得到0.9/0.9=1
如果看不懂代表你連Sigma或等比數列都不會,該回高中重讀了
簡單來說,0.9....
可以代換成0.9乘以各次方1/10的數列之和
如此一來就變成一個無窮等比數列,而代入無窮等比數列的和公式去算會得到0.9/0.9=1
如果看不懂代表你連Sigma或等比數列都不會,該回高中重讀了
無題 無名 19/05/12(日)00:58:18 ID:lgSBxmtc No.1256432
無題 無名 19/05/12(日)02:53:28 ID:QSVGv7tM No.1256488
>>1255908
單抽跟十連抽用的算法不一樣,十連的機制會因遊戲設定而異像FGO你十連抽就一定至少有一張4星,這在機率上改變就很大(禮裝還是從者又是另外問題).
但無論你多抽幾次機率還是不會變,中獎率會變動的話代表抽卡有保底機制.
所以手遊抽卡機率變動因素主要有:
- 卡池大小
- 星數/稀有度占總卡池的量
- 連抽機制是否有保證最低數量的稀有卡
- 是否有保底機制,也就是X連抽後必定會有一張超稀有卡
記得,手遊卡池並‧沒‧有‧減少/縮小概念,你能幾連抽抽到想要的只有兩種可能性: 1-該遊戲有保底機制 2-你運氣好
很多人都把手遊抽卡跟現實物理上抽獎混為一談,
現實中抽獎的票卷/籤會隨著次數減少所以中將率會逐漸變高,
但虛擬抽卡並不會,除非設計的人有設計成會減少或逐漸提高其他卡的機率,否則除了保底機制以外無論多少抽機率都一模一樣.
如果手遊抽卡機率會隨著抽的次數增加的話也不會有花幾百萬在FGO或GBF等遊戲的新聞了.
單抽跟十連抽用的算法不一樣,十連的機制會因遊戲設定而異像FGO你十連抽就一定至少有一張4星,這在機率上改變就很大(禮裝還是從者又是另外問題).
但無論你多抽幾次機率還是不會變,中獎率會變動的話代表抽卡有保底機制.
所以手遊抽卡機率變動因素主要有:
- 卡池大小
- 星數/稀有度占總卡池的量
- 連抽機制是否有保證最低數量的稀有卡
- 是否有保底機制,也就是X連抽後必定會有一張超稀有卡
記得,手遊卡池並‧沒‧有‧減少/縮小概念,你能幾連抽抽到想要的只有兩種可能性: 1-該遊戲有保底機制 2-你運氣好
很多人都把手遊抽卡跟現實物理上抽獎混為一談,
現實中抽獎的票卷/籤會隨著次數減少所以中將率會逐漸變高,
但虛擬抽卡並不會,除非設計的人有設計成會減少或逐漸提高其他卡的機率,否則除了保底機制以外無論多少抽機率都一模一樣.
如果手遊抽卡機率會隨著抽的次數增加的話也不會有花幾百萬在FGO或GBF等遊戲的新聞了.
無題 無名 19/05/12(日)03:33:16 ID:YBoZWXMk No.1256497
無題 無名 19/05/12(日)03:44:30 ID:QSVGv7tM No.1256500
無題 無名 19/05/12(日)04:54:13 ID:I2JLiz0g No.1256515
我高中生啦,0.9循環=1還可以理解,但老師給不出1的無限大次方和0的無限大次方是多少,這是怎樣?
無題 無名 19/05/12(日)07:44:52 ID:fHpVcRWg No.1256551
>>1256342
這個老爸是說 有人把答案告訴他 他還是無法理解證明的過程 所以覺得錯的答案才對
這個跟 天才 或是有經驗的高手 專家看到問題 第一時間腦中浮現的答案 (應該是包含證明的過程要往那個方向進行)
其實我覺得是差不多的東西
這個老爸是說 有人把答案告訴他 他還是無法理解證明的過程 所以覺得錯的答案才對
這個跟 天才 或是有經驗的高手 專家看到問題 第一時間腦中浮現的答案 (應該是包含證明的過程要往那個方向進行)
其實我覺得是差不多的東西
突然覺得這串可以收精華了
被抽抽機率、蒙提霍爾問題、0.9999...是否等於一問題困擾的人可以參考這串
被抽抽機率、蒙提霍爾問題、0.9999...是否等於一問題困擾的人可以參考這串
無題 無名 19/05/12(日)08:56:28 ID:Nrnjj2Wo No.1256569
無題 無名 19/05/12(日)09:51:50 ID:Pwup7Gvg No.1256582
>>1256578
也不盡然 島上神串幾乎都是看島民哪天腦洞開在對的位置 像之前那篇逆轉毒牙 原本的圖也沒什麼特別就是一篇很常見的短篇 結果就莫名其妙成了祭典了w
也不盡然 島上神串幾乎都是看島民哪天腦洞開在對的位置 像之前那篇逆轉毒牙 原本的圖也沒什麼特別就是一篇很常見的短篇 結果就莫名其妙成了祭典了w
無題 無名 19/05/12(日)10:19:58 ID:9aZWu8X. No.1256591
>>1256575
想起了以前超常(?)的量子蘿學
想起了以前超常(?)的量子蘿學
無題 無名 19/05/12(日)10:22:53 ID:QZ.0njlg No.1256592
上課囉
無題 無名 19/05/12(日)15:16:41 ID:knXYTG.U No.1256831
>>1256529
數學哥布林:違反直覺但是邏輯正確
數學哥布林:違反直覺但是邏輯正確
一開始就確定要換的話就是2/3
一開始就確定不要換的話是1/3
但是如果在換與不換之間飄忽不定的話是不是就變回1/2了
一開始就確定不要換的話是1/3
但是如果在換與不換之間飄忽不定的話是不是就變回1/2了
無題 無名 19/05/12(日)17:01:22 ID:lgSBxmtc No.1256935
>>1256919
>>但是如果在換與不換之間飄忽不定的話是不是就變回1/2了
會介於1/3與2/3之間
視乎你飄到各自選項的機率是多少而定
如果從一開始就確定你會在最後關頭擲硬幣決定你要不要換
那你的總中獎率就是50%
但如果你的飄忽不定不是用擲硬幣這種客觀機率來決定,而是看心情
那沒有人會知道你的心情的機率分佈
>>但是如果在換與不換之間飄忽不定的話是不是就變回1/2了
會介於1/3與2/3之間
視乎你飄到各自選項的機率是多少而定
如果從一開始就確定你會在最後關頭擲硬幣決定你要不要換
那你的總中獎率就是50%
但如果你的飄忽不定不是用擲硬幣這種客觀機率來決定,而是看心情
那沒有人會知道你的心情的機率分佈
無題 無名 19/05/12(日)17:23:04 ID:n0e1jHaU No.1256957
無題 無名 19/05/12(日)18:05:46 ID:aPCvzFF. No.1257090
沒證據顯示你選的不對
所以你換不換都是1/3變1/2
所以你換不換都是1/3變1/2
無題 無名 19/05/12(日)18:09:57 ID:45ukAnvA No.1257103
那我來換一個問法
假如有三扇門,其中兩扇是刑具,一扇則是什麼都沒有
你在選了一扇門後,黑道老大開了你沒選的其中一扇,後面是一架刑具
那你要不要換門?
假如有三扇門,其中兩扇是刑具,一扇則是什麼都沒有
你在選了一扇門後,黑道老大開了你沒選的其中一扇,後面是一架刑具
那你要不要換門?
無題 無名 19/05/12(日)18:20:58 ID:sWsIaP.E No.1257125
>>1257117
不是喔,你是在[1]和[x-1]之間做選擇
不是喔,你是在[1]和[x-1]之間做選擇
無題 無名 19/05/12(日)18:22:32 ID:I2JLiz0g No.1257131
無題 僅參考(?) 19/05/12(日)18:32:39 ID:ftWH1VDA No.1257153
>>1257117
把閱讀順序改下
你有三選一,挑個1/3;剩2/3
換就是包了2/3兩個門(但是主持人把這2/3裡面沒中的爆掉了),所以換了就變2/3,是一口氣選兩扇門,只是其中一扇門(沒中的)主持人先幫你開了
題目則是先描述沒中的門被開了在讓你決定換不換,其實是讓你3選1跟3選2的差別
把閱讀順序改下
你有三選一,挑個1/3;剩2/3
換就是包了2/3兩個門(但是主持人把這2/3裡面沒中的爆掉了),所以換了就變2/3,是一口氣選兩扇門,只是其中一扇門(沒中的)主持人先幫你開了
題目則是先描述沒中的門被開了在讓你決定換不換,其實是讓你3選1跟3選2的差別
無題 無名 19/05/12(日)18:54:18 ID:FmReo85s No.1257202
>>1256525
看這個
https://math.stackexchange.com/questions/319764/1-to-the-power-of-infinity-why-is-it-indeterminate
看這個
https://math.stackexchange.com/questions/319764/1-to-the-power-of-infinity-why-is-it-indeterminate
有一百萬個箱子
讓你隨便選一個
你選好後,
主持人打開了剩下的其中九十九萬九千九百九十八個
現在只剩下「原本你選好的一個」以及「主持人剩下的一個」
你覺得自己原本就從一百萬個箱子裏選中了百萬分之一的有獎箱子
的機會比較大,還是
自己原本沒有選中,有獎箱子在剩下的九十九萬九千九百九十九個裏
的機會比較大?
如果後者的機會比較大,那麼主持人把沒有中獎的九十九萬九千九百九十八個箱子都挑走了
剩下的一個箱子 和你手上的箱子 哪一個中獎的機會更大?
讓你隨便選一個
你選好後,
主持人打開了剩下的其中九十九萬九千九百九十八個
現在只剩下「原本你選好的一個」以及「主持人剩下的一個」
你覺得自己原本就從一百萬個箱子裏選中了百萬分之一的有獎箱子
的機會比較大,還是
自己原本沒有選中,有獎箱子在剩下的九十九萬九千九百九十九個裏
的機會比較大?
如果後者的機會比較大,那麼主持人把沒有中獎的九十九萬九千九百九十八個箱子都挑走了
剩下的一個箱子 和你手上的箱子 哪一個中獎的機會更大?
無題 無名 19/05/12(日)19:45:31 ID:I2JLiz0g No.1257288
1. 一開始贏的機率1/3,輸的機率2/3
2. 如果換,贏會變輸,輸會變贏
3. 所以換了之後變成:輸的機率1/3,贏的機率2/3
有哪一步看不懂的
2. 如果換,贏會變輸,輸會變贏
3. 所以換了之後變成:輸的機率1/3,贏的機率2/3
有哪一步看不懂的
>>1257294
有 要先踏左腳還是右腳你沒講清楚啊(X
有 要先踏左腳還是右腳你沒講清楚啊(X
無題 無名 19/05/12(日)19:57:52 ID:9wuHoYyM No.1257299
>>1257298
你是不是假定了我是二足步行
你是不是假定了我是二足步行
無題 無名 19/05/12(日)20:00:26 ID:5DJca.9I No.1257300
其實最後不是二選一
而是參加者和主持人持有的門全部交換
這個問題的詭計在於主持人開了一道門讓人以為是二選一
換個進行方式來看
一開始主持人有三道門,其中一道放有獎品
再來讓參加者選一道門先不打開
告訴參加者說"我剩下的兩道門中至少有一個是沒獎品的喔,有必要的話我可以打開一道沒獎品的門給你看"
當然很明顯這一句是廢話
在簡化的結果就是兩個選擇:
一邊是一道門;另外一邊是兩道門,而且可知至少一道門沒獎品(廢話)
門少和門多選當然是門多的選擇中獎機會大
而是參加者和主持人持有的門全部交換
這個問題的詭計在於主持人開了一道門讓人以為是二選一
換個進行方式來看
一開始主持人有三道門,其中一道放有獎品
再來讓參加者選一道門先不打開
告訴參加者說"我剩下的兩道門中至少有一個是沒獎品的喔,有必要的話我可以打開一道沒獎品的門給你看"
當然很明顯這一句是廢話
在簡化的結果就是兩個選擇:
一邊是一道門;另外一邊是兩道門,而且可知至少一道門沒獎品(廢話)
門少和門多選當然是門多的選擇中獎機會大
無題 無名 19/05/12(日)20:02:12 ID:j5.GKQPQ No.1257302
無題 無名 19/05/12(日)20:11:28 ID:xCZA4diM No.1257309
>>1257298
履帶孩試車輪?
履帶孩試車輪?
一開始就了解原理並堅定選擇的勝率是2/3
但是如果選擇換與不換的機率是1/2
就變成1/2的機率獲得2/3勝率的門,以及1/2的機率獲得1/3勝率的門
所以"理解"這一行為改變了機率?
但是如果選擇換與不換的機率是1/2
就變成1/2的機率獲得2/3勝率的門,以及1/2的機率獲得1/3勝率的門
所以"理解"這一行為改變了機率?
無題 無名 19/05/12(日)20:28:37 ID:9iklosvM No.1257327
高中念文組上機率課一定有老師怎麼說破嘴都一臉困惑聽不懂的學生
也有老師講一遍就通、覺得老師為什麼要浪費20分鐘繼續糾纏這問題的學生
這一串讓我回想起高中的時候......
也有老師講一遍就通、覺得老師為什麼要浪費20分鐘繼續糾纏這問題的學生
這一串讓我回想起高中的時候......
>>1257311
智力本來就會影響你做一件事情的成功率
這就像是
我叫你押注大或小,然後骰一個骰子
骰出1~4算小的贏,骰出5~6算大的贏
獲勝時賠率一樣都是乘二
智商正常的都會選小,勝率66%
但就是有些蠢蛋會去押大
你會說蠢蛋改變了機率嗎?
智力本來就會影響你做一件事情的成功率
這就像是
我叫你押注大或小,然後骰一個骰子
骰出1~4算小的贏,骰出5~6算大的贏
獲勝時賠率一樣都是乘二
智商正常的都會選小,勝率66%
但就是有些蠢蛋會去押大
你會說蠢蛋改變了機率嗎?
無題 無名 19/05/12(日)20:36:54 ID:FmReo85s No.1257334
我們這樣想吧
你選了一扇門,主持人選了兩扇門
你選1中的機率是1/3,主持人是2/3
這時兩人的中獎率就定了,不再變動了
就算主持人給你看了其中一扇他選的門(羊),也不會改變主持人選了兩扇門,中獎率是2/3的結果
當主持人開其中一扇門並問你要不要換門的時候,其實問的是要不要用你的1/3中獎率換主持人的2/3中獎率
__________上面看不懂的話
你先選一扇門,主持人再取另外兩扇
主持人得到的門可能是
AB 羊車
AC 羊羊
BC 車羊
以上可知主持人的三個可能性中其中兩個有車,中獎率是2/3
然後主持人把三個可能性的內容各剃除一隻羊,變成
AB 車
AC 羊
BC 車
主持人的中獎率還是2/3,而你的中獎率是1/3
所以用你的1/3中獎率換主持人的2/3中獎率是比較有利的
你選了一扇門,主持人選了兩扇門
你選1中的機率是1/3,主持人是2/3
這時兩人的中獎率就定了,不再變動了
就算主持人給你看了其中一扇他選的門(羊),也不會改變主持人選了兩扇門,中獎率是2/3的結果
當主持人開其中一扇門並問你要不要換門的時候,其實問的是要不要用你的1/3中獎率換主持人的2/3中獎率
__________上面看不懂的話
你先選一扇門,主持人再取另外兩扇
主持人得到的門可能是
AB 羊車
AC 羊羊
BC 車羊
以上可知主持人的三個可能性中其中兩個有車,中獎率是2/3
然後主持人把三個可能性的內容各剃除一隻羊,變成
AB 車
AC 羊
BC 車
主持人的中獎率還是2/3,而你的中獎率是1/3
所以用你的1/3中獎率換主持人的2/3中獎率是比較有利的
無題 無名 19/05/12(日)20:39:48 ID:uCIr.fVs No.1257338
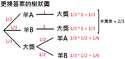
>>1254850
怎麼這串還在啊?
雖然有點不直覺,不過用上面舉例的極端情況
(100萬個箱子開了999,999個)不是很好懂?
再不然用我附圖的窮舉圖示嘛,若是3號箱子中獎
就有2/3(紅圈處)的機會是「換」會中獎
怎麼這串還在啊?
雖然有點不直覺,不過用上面舉例的極端情況
(100萬個箱子開了999,999個)不是很好懂?
再不然用我附圖的窮舉圖示嘛,若是3號箱子中獎
就有2/3(紅圈處)的機會是「換」會中獎
無題 無名 19/05/12(日)20:43:54 ID:Z/6iY2fI No.1257343
無題 無名 19/05/12(日)20:45:23 ID:Z/6iY2fI No.1257344
>>1257333
但對於蠢蛋本身來說 勝率就不是66% 還是說這是不能計算的
但對於蠢蛋本身來說 勝率就不是66% 還是說這是不能計算的
無題 無名 19/05/12(日)20:46:48 ID:T.C4L13U No.1257346
我覺得應該要先解釋"為什麼第二次的選擇不是獨立事件"
因為以一般人直觀的方式言第二次的選擇是個獨立事件
所以是在剩下的兩個選項中選擇一個
因為以一般人直觀的方式言第二次的選擇是個獨立事件
所以是在剩下的兩個選項中選擇一個
我在想沒有搞懂的人是不是這樣想
對他們來說前面獲得的情報不重要
所以選哪扇門都行,結論而言的確是1/2
不過這裡有個問題是,
這些人到底有沒有真的用1/2在選
如果因為都是1/2就堅持不換的話那就根本不是1/2機率了
要完全捨棄之前的選擇後重選的1/2才會變成真的1/2
對他們來說前面獲得的情報不重要
所以選哪扇門都行,結論而言的確是1/2
不過這裡有個問題是,
這些人到底有沒有真的用1/2在選
如果因為都是1/2就堅持不換的話那就根本不是1/2機率了
要完全捨棄之前的選擇後重選的1/2才會變成真的1/2
無題 無名 19/05/12(日)20:54:44 ID:Z/6iY2fI No.1257356
無題 無名 19/05/12(日)20:59:07 ID:lgSBxmtc No.1257364
無題 無名 19/05/12(日)21:04:37 ID:GWX3vrP. No.1257369
無題 無名 19/05/12(日)21:05:32 ID:gAXZ4Oe. No.1257371
邏輯經常是反直覺的
無題 無名 19/05/12(日)22:46:36 ID:qi6EWChM No.1257469
等一下
羊不是名器嗎?
誰知道那個大獎究竟是甚麼大獎
而且羊有兩隻耶!中獎機率比較高啊!
羊不是名器嗎?
誰知道那個大獎究竟是甚麼大獎
而且羊有兩隻耶!中獎機率比較高啊!
無題 無名 19/05/13(一)00:14:06 ID:aXjLOMVk No.1257558
無題 無名 19/05/13(一)00:45:54 ID:z3PP.VSw No.1257583
無題 無名 19/05/13(一)00:59:08 ID:XeEa8vAs No.1257591
無題 無名 19/05/13(一)01:19:52 ID:ap6mdSPg No.1257607
>>1257357
古早年代是能力分班沒錯
結果
成績好的爛人持續自我膨脹
成績好的好人被環境帶向膨脹
成績差的爛人失去變好的機會
成績差的好人在學校活的像狗
後來廣推常態分班,希望學生在學校多學學做人的道理。
就變成現在這樣了。
古早年代是能力分班沒錯
結果
成績好的爛人持續自我膨脹
成績好的好人被環境帶向膨脹
成績差的爛人失去變好的機會
成績差的好人在學校活的像狗
後來廣推常態分班,希望學生在學校多學學做人的道理。
就變成現在這樣了。
無題 無名 19/05/13(一)01:22:51 ID:kUGkCPr. No.1257608
>>1257357
因為那樣做的資源消耗量高
因為那樣做的資源消耗量高
無題 無名 19/05/13(一)02:04:20 ID:ap6mdSPg No.1257621
>>1257613
老天,這名聲豈不是臭到家了?
老天,這名聲豈不是臭到家了?
>>No.1254903
>>https://www.youtube.com/watch?v=eYmSDnVFxT4
改一下比較好理解:
100顆蘋果,其中99顆裡面長蟲
你從100顆裡先選1顆拿走,
然後攤主把剩下的98顆切開,全是有蟲的,
剩下1顆沒切開的,你換不換?
簡單來說:
場面上剩2顆,1顆是你一開始選的,1顆是最後攤主沒切開的
你一開始選的那顆是在100顆裡挑的,沒蟲的機率是1%,
攤主沒切開的那顆是最後2顆其中之一,沒蟲的機率是50%,
所以,你應該換~
>>https://www.youtube.com/watch?v=eYmSDnVFxT4
改一下比較好理解:
100顆蘋果,其中99顆裡面長蟲
你從100顆裡先選1顆拿走,
然後攤主把剩下的98顆切開,全是有蟲的,
剩下1顆沒切開的,你換不換?
簡單來說:
場面上剩2顆,1顆是你一開始選的,1顆是最後攤主沒切開的
你一開始選的那顆是在100顆裡挑的,沒蟲的機率是1%,
攤主沒切開的那顆是最後2顆其中之一,沒蟲的機率是50%,
所以,你應該換~
無題 無名 19/05/13(一)03:06:30 ID:ap6mdSPg No.1257641
>>1257637
沒蟲的機率是99%才對
沒蟲的機率是99%才對
無題 無名 19/05/13(一)03:09:38 ID:ap6mdSPg No.1257642
>>1257637
抱歉眼瞎,麻煩當我上面沒說,刪不掉。
抱歉眼瞎,麻煩當我上面沒說,刪不掉。
>>No.1254903
>>https://www.youtube.com/watch?v=eYmSDnVFxT4
影片中的結論「應該要換」是正確的,但是數字上有瑕疵
應是1/2大於1/3
不是2/3大於1/3
列舉如下:
(一)選中 開門 沒換中
(二)選中 沒換中 開門
(三)換中 沒選中 開門
(四)換中 開門 沒選中
換中跟沒換中的機率都是1/2,那些算成2/3的孩子應該是把(一)跟(二)合併了
>>https://www.youtube.com/watch?v=eYmSDnVFxT4
影片中的結論「應該要換」是正確的,但是數字上有瑕疵
應是1/2大於1/3
不是2/3大於1/3
列舉如下:
(一)選中 開門 沒換中
(二)選中 沒換中 開門
(三)換中 沒選中 開門
(四)換中 開門 沒選中
換中跟沒換中的機率都是1/2,那些算成2/3的孩子應該是把(一)跟(二)合併了
無題 無名 19/05/13(一)03:31:59 ID:GcVpoc4k No.1257645
>>No.1257643
>>列舉如下:
>>(一)選中 開門 沒換中
>>(二)選中 沒換中 開門
>>(三)換中 沒選中 開門
>>(四)換中 開門 沒選中
>>換中跟沒換中的機率都是1/2,那些算成2/3的孩子應該是把(一)跟(二)合併了
抱歉,是我弄錯了
現實情況是(一)跟(二)只能擇一作為,
換中的機率確實是2/3沒錯
>>列舉如下:
>>(一)選中 開門 沒換中
>>(二)選中 沒換中 開門
>>(三)換中 沒選中 開門
>>(四)換中 開門 沒選中
>>換中跟沒換中的機率都是1/2,那些算成2/3的孩子應該是把(一)跟(二)合併了
抱歉,是我弄錯了
現實情況是(一)跟(二)只能擇一作為,
換中的機率確實是2/3沒錯
無題 無名 19/05/13(一)03:32:59 ID:b3yhLUI. No.1257646
我不想用侮辱性的字眼
但是我很困惑你們哪來的自信修正出這種理論的
理論全錯了好嗎
重點在於第一次選擇的時候
不管是1/3還是1/100
在去除多餘數量後的第二次選擇裡
代表的是"翻轉"
而不是讓你們用2這個數字去再乘除一遍
第一次你選中的機率是1%
那麼第二次選擇代表跳槽去99%的"那一邊"
用遊戲說吧
從一到一百猜一個數字很難一次就中
但是你"已經猜了"一個數字
接下來將選項剔除
只剩下"你原本猜的只有1%機率中的數字"
還有另一個"代表著那99%個可能性合體的那個數字"
怎麼會被算成50%的機率的?
把百分之一換成三分之一也是同樣的情況。
請不要混淆概念謝謝。
但是我很困惑你們哪來的自信修正出這種理論的
理論全錯了好嗎
重點在於第一次選擇的時候
不管是1/3還是1/100
在去除多餘數量後的第二次選擇裡
代表的是"翻轉"
而不是讓你們用2這個數字去再乘除一遍
第一次你選中的機率是1%
那麼第二次選擇代表跳槽去99%的"那一邊"
用遊戲說吧
從一到一百猜一個數字很難一次就中
但是你"已經猜了"一個數字
接下來將選項剔除
只剩下"你原本猜的只有1%機率中的數字"
還有另一個"代表著那99%個可能性合體的那個數字"
怎麼會被算成50%的機率的?
把百分之一換成三分之一也是同樣的情況。
請不要混淆概念謝謝。
無題 無名 19/05/13(一)03:43:55 ID:ZdZJw1kU No.1257650
>>1257643
我剛開始也覺得是1/2, 後來才發覺這不對
其實你也落入了邏輯盲點
而上面所有想解釋2/3的人沒成功說服的關鍵在於
他們都想用數字去解釋邏輯問題
這只會讓邏輯沒理解的人愈是混亂
其實只要換成文字就可以比較簡單理解了
先無視所有數字, 只要記著一個前題
"只要你一開始沒抽中大獎, 那你交換後就必定是中大獎"
只要你抽中羊, 交換後必定是車
除非你一開始抽中的就是車, 不然交換後就絕對不會是羊
所以只要沒抽中大獎的機率是多少, 那交換後是大獎的機率就有多少
我剛開始也覺得是1/2, 後來才發覺這不對
其實你也落入了邏輯盲點
而上面所有想解釋2/3的人沒成功說服的關鍵在於
他們都想用數字去解釋邏輯問題
這只會讓邏輯沒理解的人愈是混亂
其實只要換成文字就可以比較簡單理解了
先無視所有數字, 只要記著一個前題
"只要你一開始沒抽中大獎, 那你交換後就必定是中大獎"
只要你抽中羊, 交換後必定是車
除非你一開始抽中的就是車, 不然交換後就絕對不會是羊
所以只要沒抽中大獎的機率是多少, 那交換後是大獎的機率就有多少
>>1257653
其實那是很正常的達克效應,只理解到一點點的自信心膨脹,所以沒什麼好失望氣餒,那是人性的一部分
其實那是很正常的達克效應,只理解到一點點的自信心膨脹,所以沒什麼好失望氣餒,那是人性的一部分
>>1257433
推這句
主持人有沒有在你第一次選完後主動去掉一道門決定概率是從1/3變成2/3還是1/3變成1/2的決定因素.
-變成2/3的前提是[沒人知道第一次會選錯]
-變成1/2的前提是[有人知道第一次會選錯]
會讓人搞不懂比較像是出題的語病陷阱.
總之,機率概率都只是給你個基準.
就像讓電腦亂數選10次黑或白不代表一定會黑白各5次,連續10次單純黑或單純白都是有可能.
但抽更多次的話的確黑跟白的數量會接近五五波.
推這句
主持人有沒有在你第一次選完後主動去掉一道門決定概率是從1/3變成2/3還是1/3變成1/2的決定因素.
-變成2/3的前提是[沒人知道第一次會選錯]
-變成1/2的前提是[有人知道第一次會選錯]
會讓人搞不懂比較像是出題的語病陷阱.
總之,機率概率都只是給你個基準.
就像讓電腦亂數選10次黑或白不代表一定會黑白各5次,連續10次單純黑或單純白都是有可能.
但抽更多次的話的確黑跟白的數量會接近五五波.
無題 無名 19/05/13(一)04:12:02 ID:RBwsQFHg No.1257658
無題 無名 19/05/13(一)04:18:37 ID:M8SIWIvo No.1257659
無題 無名 19/05/13(一)05:30:18 ID:ZdZJw1kU No.1257676
無題 無名 19/05/13(一)05:33:32 ID:NvJVwq0E No.1257677
無題 無名 19/05/13(一)05:40:41 ID:M8SIWIvo No.1257681
無題 無名 19/05/13(一)07:05:53 ID:GovbyowI No.1257692
無題 無名 19/05/13(一)07:16:55 ID:3Ji3Ysug No.1257693
如果只考慮最後的兩道門的「單一事件」
那的確是1/2
但現在考慮最初選哪一道門這個「事件」
那的確是1/2
但現在考慮最初選哪一道門這個「事件」
也就兩種情況啊:
1.「你第一抽沒中」->主持人將其它門打開,只剩中獎那扇->換了就中獎
2.「你第一抽就中」->主持人將其它門打開,只剩沒中獎那扇->換了就摃龜
不管門是三扇還是一千扇
你認為你第一抽就中的機率有多高?
1.「你第一抽沒中」->主持人將其它門打開,只剩中獎那扇->換了就中獎
2.「你第一抽就中」->主持人將其它門打開,只剩沒中獎那扇->換了就摃龜
不管門是三扇還是一千扇
你認為你第一抽就中的機率有多高?
這串真是有夠長,而且討論還一直跳針回去
為什麼要跟這種理解不了數學的文組講那麼多啊
為什麼要跟這種理解不了數學的文組講那麼多啊
無題 無名 19/05/13(一)10:15:07 ID:QohwPdcM No.1257751
無題 無名 19/05/13(一)11:07:35 ID:HlOV/zFw No.1257790
這個換門問題在島上討論過好幾次了
每次都有人不相信理論不肯做實驗堅持是1/2
開始懷疑是不是有人在裝不懂釣魚
每次都有人不相信理論不肯做實驗堅持是1/2
開始懷疑是不是有人在裝不懂釣魚
無題 無名 19/05/13(一)12:40:59 ID:4Miof6ec No.1257879
>>1257747
等等…你好像誤會了什麼……
等等…你好像誤會了什麼……
無題 無名 19/05/13(一)12:42:14 ID:aXjLOMVk No.1257880